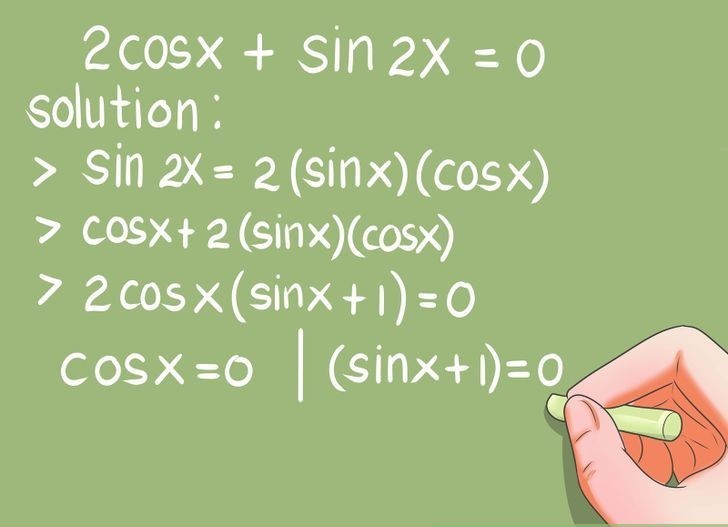Trigonometric Equations

 

Table of Content

How do the Trigonometric Equations look like? What is the difference between the principal solution and general solution? What are the general solution of basic Trigonometric Equations? How do you solve Trigonometric Equations? Is there something like trigonometric inequalities? What is a trigonometric identity? What are the Trigonometric Functions?

 

How do the Trigonometric Equations look like?

Trigonometric Equations are the equations involving one or more trigonometric ratios of unknown angle. These trigonometric ratio can be any one from the six trigonometric ratios as sine, cosine, tangent, cotangent, secant and cosecant.

Example

sin x = 0, cos² 2x + 2 sinx + 1 = 0

From the above examples, it is very much clear that the variable in the above equation is the angle x. So, for the trigonometric equation sin x = 0, we will have to find the all the possible values of x for which sin x = 0.

What is the difference between the principal solution and general solution?

The concept of principal and general solution is derived from the periodic property of trigonometric ratios. As the sine and cosine are periodic with period 2π and the tangent is periodic with period π. Thus we not only one any specific value of x for which sin/cos or tan has unique value but we have multiple values.

Refer the figure on the right to understand the concept more clearly. The figure represent the graph of sin x. and the horizontal line indicates the equation sin x = 0.5, so we can see that just in the period from 0 to 180 degree, we have got values of x (that is, 30 and 150 degrees) for which sin x = 0.5. So in a period from 0 to 360 degree, we have got two values or solutions.

So as to standardize, the principal solutions are the solutions for which the value of unknown angle x lies in the interval [0, 2π)  or 0 ≤  x < 2π. And the solutions involving an integer ‘n’ which gives all the possible solution of any particular equation are called the General Solutions.

Example 

Find the principal and general solution for: sin x = 0

Sol. sin x = 0 at x = ……, -2π, -π, 0, π, 2π, 3π, 4π …….. nπ

Thus principal solution will be: 0 and, π, while the general solution will be nπ, where n ∈ Z.
 

What are the general solution of basic Trigonometric Equations?

Let us take few basic equations one by one and analyze them.

• sin A = sin B 

So, from the above we can conclude that, For

• cos A = cos B

​Again,

So, from the above we can again conclude that, For

• tan A = tan B

​

So the above examples will help you to understand the basic of solving trigonometric equations. Below we are tabulating the general solutions of all the basic trigonometric equations.

Trigonometrical Equation	General Solution
sin A = 0	A = nπ
cos A = 0	A = (2n + 1) π/2
tan A = 0	A = nπ
sin A = 1	A = 2nπ + π/2
sin A = sin B	A = nπ + (-1)n B
cos A = cos B	A = nπ ± B
tan A = tan B	A = nπ + B
sin2 A = sin2 B cos2A = cos2B	A = nπ ± B A = nπ ± B
tan2 A = tan2 B	A = nπ ± B
sin A = sin B cos A = cos B	A = 2nπ + B
sin A = sin B tan A = tan B	A = 2nπ + B
tan A = tan B cosA = cos B	A = 2nπ + B

How do you solve Trigonometric Equations?

Solving Trigonometric Equations requires very careful observation about the given equation. As different types of equations have different approach to get its solutions in a simple manner. So here we will discuss seven important types of trigonometric equations and the way to solve them.

Type - I

In the first type, we shall discuss about the equations which can be factorized or given in terms of multiplication of factor or can be expressed in quadratic form.

Example 

(1 + cos⁡x )(1 – cot⁡ x) = 0, 3 cos²⁡x – 10 cos⁡x + 3 = 0

These types of equations can be solved by first converting them into factors (if not given directly) and then finding the solution for each factors separately. The final solutions will be the union of solutions of all the factors.

Type – II

This is a special and very important type of equation, where the equation can be expressed in the form of a cos⁡A + b sin⁡ B = c.

Example

To solve these types of equations, we first convert the given equation into the standard form that is,

a cos⁡A + b sin⁡B = c (if not given). 

Assume, a = r cos⁡∅ and b = r sin⁡∅, so that we can say

On substituting the above assumptions in the standard equation, we get

r cos⁡∅  cos⁡A + r sin⁡∅ sin⁡B = c

Now from here, we can just use the formula for cos (A – B) to simplify above and get its solutions.

 

Type - III

In the third type, we will consider the equations where we need to transform trigonometric functions from sum into product form.

Example

 sin x + sin 5x = sin 2x + sin 4x

In the above problem, the angles are different and if we just the formulas of sin C + sin D, then here we may get any one angle common on both sides.

Type - IV

This type is just the reverse process of the last type – III. Here we need to transform trigonometric functions from product to sum form.

Example

sin⁡3A = 4 sin⁡A sin⁡2A sin⁡4A

To simplify and solve this types of questions, we need to convert the given product terms of trigonometric ratios into sum to simplify it.

Type - V

In few problems, we may need to either change the variable or use substitution to solve them. Here we have one of the special substitution, where if any equation involving f(sin x ± cos⁡ x, sinx cosx) = 0, where f(x, y) is a polynomial, can be solved by substituting

sinx ± cos⁡x = t 

Further, we can write the same as,

1 ± 2 sinx cos⁡x = t²

Or 

Example

sin⁴2x + cos⁴ 2x = sin⁡²x cos⁡2x

This equation can be solved by using substitution exampled above.

Type - VI

In this sixth type, we will you the concept of boundedness to solve the problem. This concept can not be used randomly but only for the special cases.

For this type, we must remember that,

• - 1 ≤ sin⁡x ≤1, - 1 ≤ cos⁡x ≤1

• tan⁡ x ∈R, cot⁡x ∈ R

• | cosec x|  ≥ 1, | secx | ≥ 1

Example

cos x + cos2x + cos 3x = 3

In this problem, we can clearly see that, cos x + cos 2x + cos 3x = 3 only if all the terms i.e. cos x, cos 2x and cos 3x all are simultaneously equal to 3.

Type - VII

Here again, in this type we have a special form

So, for this type, we just need to use two basic conditions:

• f(x) ≥  0,  ∅ (x) ≥ 0

• f² (x) = ∅(x)

Example

 

Is there something like trigonometric inequalities?

Yes, Trigonometric inequalities are just like linear inequalities with the difference of having trigonometric ratios instead of normal variables. These inequalities are of the form P(f(x), g(x), … ) > (or <) 0, where f(x) and g(x) can be any trigonometric functions.

We need to go step by step to solve these inequalities. The steps are as follows:

• Given the function, first find its fundamental period and then draw its graph for that interval.

• For, f(x) ≤ a or f(x) ≥ a, draw a line y = a which will help us to set the range or interval.

• Using the line drawn the previous step, just take the portion of graph which satisfies the given inequality. This will give us the principal solution.

• For the general solution, we just need to add the n times the fundamental period (p) that is, np, with the fundamental period. 

Example

What is a trigonometric identity?

Identity in mathematics, is a relation or equation which is true for any value of is variable. So the trigonometric identity is a trigonometric identity involving trigonometric ratios which is satisfied for any value of its variable.

Below are few important identities, which is used to simplify the complex trigonometric equations.

• sin(A + B).sin⁡(A – B) = sin²A – sin²⁡B = cos²⁡B – cos²⁡A

• cos(A + B).cos⁡(A – B) = cos²⁡A – sin²⁡B = cos²⁡B – sin²⁡A

• sin⁡A sin(60°- A)  sin⁡ (60°+ A) = 1/4 sin⁡3A

• cos⁡A cos⁡(60° –  A) cos⁡(60° + A) =1/4 cos⁡3A

• tan⁡A tan⁡(60°- A) tan(60°+ A) = tan⁡3A

Note:- All these above identities can be easily derived by using compound angles formulae.
 

What are the Trigonometric Functions?

Trigonometric Functions, in mathematics, are the functions which help us to understand the triangle and its property more preciously. These are the functions of angle of the triangle and relates the angle with the side length of the triangles. Trigonometric functions are also called as the Circular Functions.The basic trigonometric functions in mathematics are sine, cosine and tangent functions. All the functions are basically defined considering right angled triangle but can be easily used in general.
 

Watch this Video for more reference

Related Resources:

• Look into the Revision Notes on Trigonometry for a quick revision.

• Click here for the past year papers with solutions.

• Various recommended books of Mathematics are just a click away.

To read more, Buy study materials of Trigonometry comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Mathematics here.

More Readings

Trigonometric Equation