Angles
Table of Content |
Define Trigonometry
The word trigonometry is derived from the three Greek words
In the ancient sense trigonometry defines relation between elements of a triangle. In a triangle, there are six basic elements, three sides and three angles. Any three lines segments will form a triangle iff they satisfy three triangular inequalities that is, the sum of any two lines segment is greater than third side. In Euclidean geometry, the sum of three angles of a triangle is 180°. These requirements impose limitations on the manner in which the relations between the elements are defined.
Explain Angles in Trigonometry
An Angle is a primary element in trigonometry which plays an very important rule. It is a measure of rotation of one side with respect to its initial or standard position.
For Angle measurement, we always refer two sides both of which have common termination point called as Vertex. Vertex is also referred as the point of rotation. One side which is taken as a reference (original ray) is called as the Initial Side while the other is called as the Terminal Side.
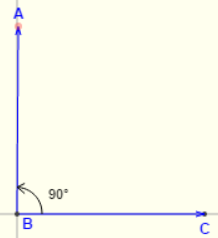
Look the figure below to understand the basic concept of angle. Side BC is called as the Initial Side and is generally towards the x – axis. Side AB is called as Terminal Side and the angle is measure between these two sides. Point B (at Origin) is the vertex and is also the point about which the terminal side is considered to be rotated.
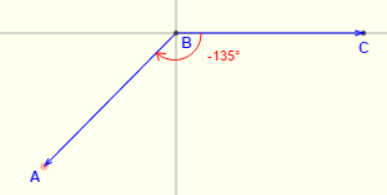
If the side AB is rotated in anticlockwise direction, then the angle is considered to be positive while for clockwise direction, the angle is negative. This can be seen in the next two figures.
 |
 |
What is the System of Angle Measurement?
We have three different systems for the angle measurement. They are as:
French System is rarely used and thus we shall only focus on English and circular system in detail the next section.
English Section: 90°
One right angle = 90° (degree)
1° = 60’ (minutes)
1’ = 60’’ (Seconds)
Circular System:
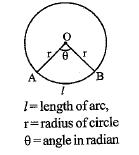In this system of measurement, angle is measured in radians. One radian is the angle made by an arc on the centre of a circle having arc length and radius equal.
Here we have, l = r. θ
The variables used in the above equation are explained in the figure.
Note:-
-
Area of sector of a circle
Explain degree measure for Angles
One complete rotation of a line about a fixed point called Vertex is considered as 360°.
Thus,
One complete rotation = 360°.
Thus, 
of a rotation from the initial to terminal side. Further, the degree is divided into minutes and minutes into seconds. One degree is considered as 60 minutes and one minute as 60 seconds. One minute is written as 60 and one second as 1’’.
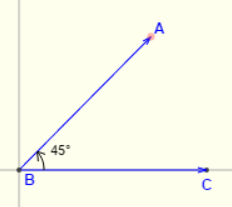
See the below figures for the examples of 0°, 90°, 180°, 270°, -135°.
Explain radian measure for Angles
Radian (or circular measurement) is based on the radius of circle. If the radius and arc lengths are equal, arc is said to subtend measure of 1 radian angle at the centre.
Angle in radian is also equals to the arc length of a circle whose radius is unity.
For a circle, circumference = 2π
If r = 1 ⇒ C = 2π ⇒ θ = 2π (in radian)
Thus, one complete circle is considered to subtend 2π radians and a half circle subtends π radians at the centre.
Radian is represented by the symbol rad or c. This superscript letter C is used for circular system.
Examples: 1 rad, 1.5 rad, 2c.
How can we relate radian with real numbers?
To relate radian measure with the real numbers, consider a circle of unit radius that is, r = 1. ‘O’ be its centre. Now consider a straight real numbered line PAQ assuming A to be its centre (or origin) point. AP be its positive side and AQ be its negative side, that is the numbers towards AP will be positive numbers and negative towards AQ.
Let this line is tangent to the considered circle and point A being its point of contact. Since from the definition of radian, if we wrap the line towards arc or if we rotate circle on number line, the distance moved by the circle on real number line will be equal to the radian measure for that corresponding length of arc.
Rotating circle towards AP will give us the positive angle while towards AQ will give the negative angle. By the simple definition of radian, we have related radian with the real numbers.
What is the relation between degree and radian?
We have seen above that, a complete rotation about a circle equals 2π radians angle. Also from our basics of circle, we know that the angle in degrees for the complete circle is 360°.
So,
2π (radians) = 360° (degrees) or π (radians) = 180° (degrees)
Assuming, π = 3.14159
Let’s take few examples to understand this conversion clearly.
Example 1: Convert 270° degrees in radians
Since we know that,
Example 2: Convert π/6 in degrees
Taking the help from,
See the table below for few more examples on relation between radian and degree measure
What is the Notational convention for Angles?
As we frequently use degrees and radians measure for the angle measure, we must understand the way they are expressed. For the degree notation, we use ‘ o ‘ notation. For Example, in angle xo this means x degrees. While for radians, generally we do not use any separate symbol. So, for radians we simply write angle x.
So, if we are writing π/3 = 60°, this means, π/3 radians is equivalent to 60°. So that means, here by default we understand that π/3 is in radian.
So from the above understanding we can generalize that,
The above relation between radian and degree measurement also help us in converting degree to radian and radian to degree measurement.
More Readings