Trigonometric Functions | IIT JEE Cosq Formulas

 

Table of Content

Some Basic Results Trigonometric Ratios of any Angle Basic Formulae

 

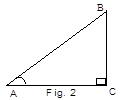
 In a right angled triangle ABC, ∠CAB = A and ∠BCA = 90° = p/2. AC is the base, BC the altitude and AB is the hypotenuse. We refer to the base as the adjacent side and to the altitude as the opposite side. There are six trigonometric ratios, also called trigonometric functions or circular functions. With reference to angle A, the six ratios are:

Obviously, .

The reciprocals of sine, cosine and tangent are called the cosecant, secant and cotangent of A respectively. We write these as cosec A, sec A, cot A respectively.

 Important Notes:

• Since the hypotenuse is the greatest side in a right angle triangle, sin A and cos A can never be greater than unity and cosec A and sec A can never be less than unity.

• All the six trigonometric functions have got a very important property in common that is periodicity. Remember that the trigonometrical ratios are real numbers and remain same as long as the angle remains same.
   

Some Basic Results

• cos²A + sin²A = 1    

From this formula, we can also derive cos²A = 1 - sin²A or sin²A = 1 - cos²A

• 1 + tan²A = sec²A    

So, from this it follows that sec²A - tan²A = 1

• cot²A + 1 = cosec²A  or  cosec²A - cot²A = 1
•  
• Fundamental inequalities: For 0 < A <, 0 < cosA <   <.
• It is possible to express trigonometrical ratios in terms of any one of them

                  e.g. 

Trigonometric Ratios of any Angle

Consider the system of rectangular co-ordinate axes dividing the plane into four quadrants. A line OP makes angle q with the positive x-axis. The angle q is said to be positive if measured in counter clockwise direction from the positive x-axis and is negative if measured in clockwise direction. The positive values of the trigonometric ratios in the various quadrants are shown, the signs of the other ratios may be derived. Note that ∠xoy = p/2, ∠xox' = p , ∠xoy' = 3p/2

P_iQ_i is positive if above the x-axis, negative if below the x-axis, OP_i is always taken positive. OQ_i is positive if along positive x-axis, negative if in opposite direction.

(Where i = 1, 2, 3, 4)

Thus depending on signs of OQ_i and P_iQ_i the various trigonometrical ratios will have different signs.

TABLE

a equals	sin a	cos a	tan a	cot a	Sec a	cosec a
–q	– sinq	cosq	–tanq	– cotq	secq	–cosec q
90° – q	cosq	sinq	cotq	tanq	cosecq	secq
90° + q	cosq	– sinq	–cotq	– tanq	–cosecq	secq
180°– q	sinq	– cosq	– tanq	– cotq	– secq	cosecq
180°+ q	– sinq	– cosq	tanq	cotq	– secq	–cosecq
360°– q	– sinq	cosq	– tanq	– cotq	secq	–cosecq
360°+ q	sinq	cosq	tanq	cotq	secq	cosecq

Note:             

• Angle q and 90°–q are complementary angles, q and 180°–q are supplementary angles
• sin(np + (–1)ⁿq) = sinq, n ÎI
• cos(2np ± q) = cosq, n ÎI
• tan(np + q) = tanq,  n ÎI

i.e. sine of general angle of the form np + (–1)ⁿq will have same sign as that of sine of angle q and so on. The same is true for the respective reciprocal functions also.

Basic Formulae

Table 1

• sin (A + B) = sin A cos B + cos A sin B
• sin (A – B) = sin A cos B – cos A sin B
• cos (A + B) = cos A cos B – sin A sin B
• cos (A – B) = cos A cos B + sin A sin B
•  
• 
• sin (A + B) sin (A – B) = sin² A – sin² B = cos² B – cos² A
• cos (A + B) cos (A – B) = cos² A – sin² B = cos² B – sin² A
• sin2A = 2sinA cosA =
• cos2A = cos²A - sin²A = 1-2 sin²A = 2cos²A-1 =
• tan2A =
• sin3A = 3sinA - 4sin³A = 4sin(60° - A) sinAsin(60° + A)
• cos3A = 4cos³A - 3cosA = 4cos(60° - A) cosAcos(60°+A)
• 

 Table 2

•  
• 
• 
• 
• tanA + tanB =
• 2sinAcosB = sin(A + B) + sin (A - B)
• 2cosAsinB = sin(A + B) - sin (A - B)
• 2cosAcosB = cos(A + B) + cos(A - B)
• 2sinAsinB = cos(A - B) - cos (A + B)

Illustration : If in a DABC, cos³A + cos³B + cos³C = 3cosA cosB cosC, then prove that the triangle is equilateral.

Solution:  Given that cos³A + cos³B + cos³C – 3cosA cosB cosC = 0

Þ (cosA + cosB + cosC) (cos²A + cos²B + cos²C – cosAcosB – cosB cosC – cosCcosA) = 0

Þ cos²A + cos²B + cos²C – cosAcosB – cosBcosC – cosCcosA = 0

(as cosA + cosB + cosC = 1 + 4 sinA/2 sinB/2 sinC/2 ¹ 0)

Þ (cosA – cosB)² + (cosB – cosC)² + (cosC – cosA)² = 0

Þ cosA = cosB = cosC

Þ A = B = C, Q 0 < A, B, C < p.

ÞDABC is equilatral.
 

Illustration:        If  , prove that tan2q = 2tan(3q + a).

Solution:     = k

  

 = =

Again 

=      \

=\ tan2q = 2 tan(3q + a).

 

Illustration :  For  any  real q , find the  maximum value  of  cos²( cosq)  + sin²(sinq) .

Solution:  The  maximum  value of  cos²( cosq) is  1  and  that  of  sin²( sinq) is  sin²1, both exists   for  q = p/2. Hence maximum value is 1+ sin²1.
 

Illustration 5:  If   .

Solution:     Þ tan²q = 1/11

 now, = 3 – 4 sin²q =  3 - 4

 
Illustration :  If A, B,C and D are angles of a quadrilateral and sin A/2  sin  B/2. sin C/2. sin D/2 = prove that A = B = C = D = π/2.

Solution:   Given 

Since, A + B = 2 - (C + D), the above equation becomes,

    = 1

 

   = 0.

This is quadratic equation in cos which has real roots.

0

4

  Now both cos and cos 1

  A = B, C = D.

Similarly, A = C, B = D  A = B = C = D = /2.

Illustration : If A, B and C are angles of a triangle, prove that

Solution:  Since  A + B + C =

=

= 

= 

as A, B, C are angles of 0 < A, B, C <

 sin A, sin B, sin C > 0

E 2 + 2 + 2    

E 6

Watch this Video for more reference
 

Illustration :  If cos(A + B) sin (C + D) = cos(A – B) sin(C – D),

prove that cotA cotB cotC = cotD.

Solution: We have cos (A + B) sin(C + D) = cos(A – B) sin(C – D)

i.e.

or

cotA cotB = tanC cotD

or cotA cotB cotC = cotD.

Illustration :  Show that 

Solution:                

LHS =

Let = a

= cos a cos 2a cos 3a cos 4a cos 5a

= – cos a cos 2a cos 4a cos 8a cos 5a

= – cos 2⁰a cos 2¹a cos 2²a cos 2³a cos 5a

= – cos 5a = –

=.

 

Illustration : Prove that cot 7   =  

Solution:  Let q = 7 Þ 2q = 15⁰

 Now cot q =

 = = .

 For more, you can also refer the papers of previous years.

 

Illustration :   If 2tan² a tan² b tan² g + tan² a tan² b + tan² b tan² g + tan² g tan² a = 1, prove that sin² a + sin² b + sin² g = 1.

Solution: ÞWe have, 2tan²a tan²btan²g + tan²atan²b + tan²btan²g + tan²gtan²a = 1

Þ 2 + cot²g + cot²a + cot²b = cot²a cot²b× cot²g

Þ cosec²a + cosec²b + cosec²g – 1

= (cosec²a – 1) (cosec²b – 1) (cosec²g – 1)

Þ cosec²a + cosec²b + cosec²g – 1

= – 1 + cosec²a + cosec²b + cosec²g – (cosec²a cosec²b + cosec²b cosec²g  + cosec²gcosec²a + cosec²a× cosec²b× cosec²g

cosec²a cosec²b + cosec²b× cosec²g + cosec²g cosec²a

= cosec²a cosec²b× cosec²gÞ sin²a + sin²b + sin²g = 1