Trigonometric Ratios Positive and Negative Angles| IIT JEE Trigonometry Positive and Negative Angles

 

By convention, an angle is defined to be positive when it is measured in anticlockwise direction with respect to the positive x-axis. Similarly, when an angle is measured in the clockwise direction from the positive x- axis it is considered to be negative. The concept runs parallel to that of coordinates in the Cartesian system where the distances to the right of origin are considered positive while that to the left are considered negative. The figures listed below clarify the concept of negative angles:

Now, we formulate the relationship between trigonometric angles i.e. between positive and negative angles. From the figure given below, we derive the following:                   

sin θ = P/H = y/√x² +y², and

sin (–θ) = (-y)/√x² + y² = –sin θ

∴ sin (–θ) = –sin θ

Similarly,

cos θ = B/H = x/√x² + y², and

cos (–θ) = x/√x² + y² = cosθ

∴ cos (–θ) = cos θ

Periodicity and the related properties

A function f(x) is said to be periodic if there exists some p such that f(x) = f(x + p) for all x and some fixed p. Here p is called the period of f. Some of the examples of periodic functions are listed below:

1. The cosine function is periodic with period 2π.

2. The constant function is periodic with no period. The reason behind this is that it satisfies the condition f(x+T) = f(x) for all x but there is no minimum value of T which can be called period.

3. If the period of f(x) is T then that of k f (ax+b) is T/|a|, hence period is affected by coefficient of x only.

4. Inverse of a periodic function in general does not exist. But the scenario is different in case of trigonometric functions. Since their range and domain are definite so their inverse exists.

5. If f(x) has its period T and g(x) has its period M, then (a f(x) + b g(x)) has its period < L.C.M. (T, M). Moreover if f(x) and g(x) are basic trigonometric functions then period of  [af (x) + bg(x)] = L.C.M. (T, M).

6. If a constant is added, subtracted, multiplied or divided in a periodic function, its period is unaffected.

7. The periods of some of the common functions are listed below:

           Function                                                                                        Period

           sin (ax + b), cos (ax + b), sec (ax + b), cosec (ax + b)           2π/a

           tan (ax + b), cot (ax + b)                                                              π/a

           |sin (ax + b), cos (ax + b), sec (ax + b), cosec (ax + b)|        π/a

           |tan (ax + b), cot (ax + b)|                                                           π/2a

Illustration:

Examine whether sin x is a periodic function or not. If yes, find its period.

Solution:

Given f(x) = sin x. Let’s assume sin x to be periodic. Then, by definition there must exist some positive value independent of x say P such that

f(x + P) = f(x)

⇒ sin (x + P) = sin x

⇒ x + P = n π + (–1)ⁿ x where n = 0, + 1, + 2 ………

The positive values of T independent of x are given by n π where

n = 2, 4, 6………

Moreover, according to the definition of periodic number, it should be least. So, here we have T = 2π.

Thus, it is proved that sin x is periodic function having periodicity 2π.

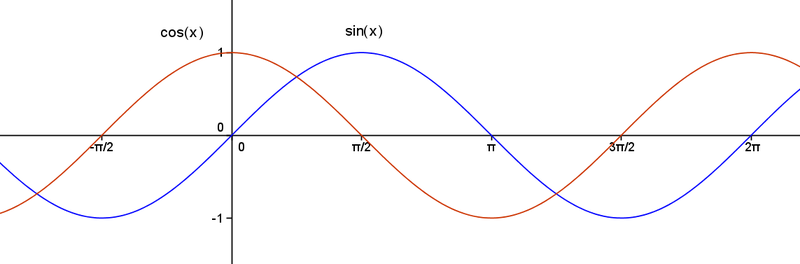
Remark: The proof of cos x also follows on the same lines. It is clear from the graph of sin x and cos x given below that both of them are periodic functions.

 

Illustration:

Let f(x) = x – [x] where [x] is the greatest integer less than or equal to x.

Find out the periodicity of f(x).

Solution:

Since the function is periodic, so it follows that

f(x + T) = f(x)

⇒ (x + T) – [x + T] = x – [x]

⇒ T = [x + T] – [x] = an integer.

Hence least positive value of T independent of x is 1.

Thus f(x) is a periodic function with period 1.

To read more, Buy study materials of Inverse Trigonometric Functions comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Mathematics here.