Factors Affecting Rate of Reaction
Table of Content |
|
|
Nature of the Reactants
(i) Physical State of Reactants
-
Decreasing rate of reaction: Gaseous state> Liquid state>Solid state
-
In a heterogeneous system collision is not so effective as in homogenous system. Thus, reactions in liquid phase or solution phase will be faster in comparison to heterogeneous conditions when same concentrations of the reactants are taken.
(ii) Physical Size of the Reactants
-
Among the solids, rate increases with decrease in particle size.
-
In powdered state rate of reaction is maximum because in powdered state, surface area is maximum.
(iii) Chemical Nature of Reactants
-
Consider the following two reactions:
2NO(g) + O2(g) → 2NO2(g) ...... (i)
CH2(g) + 2O2(g) → CO2(g) + 2H2O ..... (ii)
-
The first reaction is faster than the second because in the first reaction only N ≡ O bond is to be broken where as in the second reaction four (C-H) bonds are to be broken.
-
Similarly consider another example of two similar reactions:
2NO(g) + O2(g) → 2NO2(g) ...... (iii)
2CO(g) + 2O2(g) → 2CO2(g) ...... (iv)
-
NO bond is weaker than CO bond, hence broken easily. Thus reaction (iii) is faster than (iv).

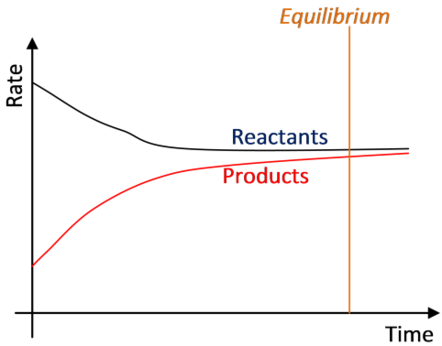
Concentration of Reactants
-
Let us consider the reaction:
A + B → C + D; Rate = k[A][B]
-
Rate of the above reaction decreases with the passage of time because the concentration of reactants A and B will decrease as time pass on.
-
Let us consider the following reversible reaction: A + B ↔ C + D
-
Rate of forward reaction = kf[A][B]
-
Rate of backward reaction = kb[C][D]
-
Rate of forward reaction decreases and that of backward reaction increases with passage of time.
-
At equilibrium both the rates become equal.
Refer to the following video for factors affecting rate of reaction
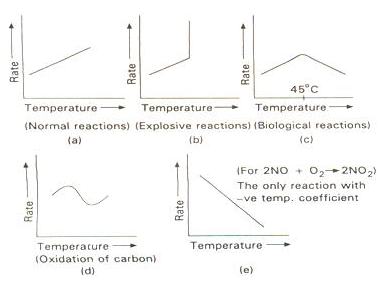
Effect of Temperature
-
The rate of reaction increases considerably with an increase in temperature.
-
The rates of many reactions are approximately doubled or tripled for every 10oC rise in temperature.
-
The temperature coefficient of a chemical reaction is defined as the ratio of the specific reaction rates of a reaction at two temperature differing by 10oC.
-
μ = Temperature coefficient= k(r+10)/kt
-
Let temperature coefficient of a reaction be ' μ ' when temperature is raised from T1to T2; then the ratio of rate constants or rate may be calculated as
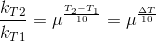
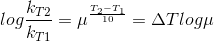
![\frac{k_T_2}{k_T_1}= antilog[\frac{\Delta T}{10 }] log\mu](https://files.askiitians.com/cdn1/cms-content/common/latex.codecogs.comgif.latex_frack_t_2k_t_1antilog_frac_deltat10log_mu.jpg)
Its value lies generally between 2 and 3.
In order to explain the effect of temperature on the reaction rate. Arrhenius proposed a theory of reaction rate which states as follows :
-
A chemical reaction takes place by collision between the reactant molecules, and collision to be effective the colliding molecules must posses some certain minimum energy called threshold energy of the reaction.
-
Reactant molecules having energy equal or greater than the threshold are called active molecules and those having energy less than the threshold are called passive molecules.
-
At a given temperature there exists a dynamic equilibrium between active and passive molecules. The process of transformation from passive to active molecules being endothermic, increase of temperature increases the number of active molecules and hence the reaction.
Passive molecules  Active molecules, DH = +ve
Active molecules, DH = +ve
-
Concept of energy of activation (Ea)
-
The extra amount of energy which the reactant molecules (having energy less than the threshold) must acquire so that their mutual collision may lead to the breaking of bond(s) and hence the reaction, is known as energy of activation of the reaction. It is denoted by the symbol Ea. Thus,
Ea = Threshold energy – Actual average energy
Ea is expressed in kcals mole–1 or kJ mole–1.
-
The essence of Arrhenius Theory of reaction rate is that there exists an energy barrier in the reaction path between reactant(s) and product(s) and for reaction to occur the reactant molecules must climb over the top of the barrier which they do by collision. The existence of energy barrier and concept of Ea can be understood from the following diagram.
? = Summation of enthalpies of reactants
= Summation of enthalpies of reactants
 ?= Summation of enthalpies of products
?= Summation of enthalpies of products
 H = Enthalpy change during the reaction
H = Enthalpy change during the reaction
Ea1 = Energy of activation of the forward reaction (FR)
Ea2 = Energy of activation of the backward reaction (BR)
Collision frequency is the number of collisions per unit volume per unit time. It is denoted by the symbol Z. Z is directly proportional to ÖT. By 10° rise in temperature. So, it is the fraction of the total number of effective, collisions that increases markedly by 10° rise in temperature resulting into marked increase in the reaction rate.

Catalyst
A catalyst is a substance, which increases the rate of a reaction without itself being consumed at the end of the reaction, and the phenomenon is called catalysis. There are some catalysts which decrease the rate of reaction and such catalysts are called negative catalyst. Obviously, the catalyst accelerating the rate will be positive catalyst. However, the term positive is seldom used and catalyst itself implies positive catalyst.
Catalyst are generally foreign substances but sometimes one of the product formed may act as a catalyst and such catalyst is called “auto catalyst” and the phenomenon is called auto catalysis.
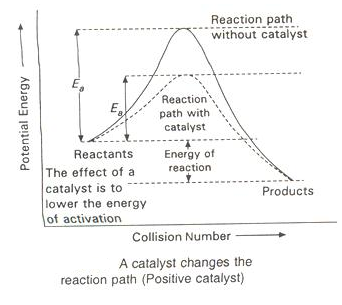
Presence of a Positive Catalyst
-
The function of a positive is to lower down the activation energy.
-
The greater the decrease in the activation energy caused by the catalyst, higher will be the reaction rate.
-
In the presence of a catalyst, the reaction follows a path of lower activation energy. Under this condition, a large number of reacting molecules are able to cross over the energy barrier and thus the rate of reaction increases.
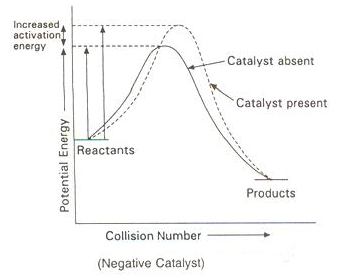
Presence of Negative Catalyst
-
A negative catalyst increases the activation energy of reaction by forming a new intermediate of high energy, i.e., by changing the reaction mechanism.
-
Due to increased activation energy, some active molecules become inactive, therefore, rate of reaction decreases.
Let 'p' denote presence of catalyst and 'a' denote absence of catalyst.
kp = Ae-Ep/RT .... (i)
ka = Ae-Ea/RT ... (ii)
Dividing (1) by (2), we get
kp/ka = e(Ea - Ep )/RT = e?E/RT
kp/ka = Antilog[?E/(2.303 RT)]
Solved Example |
|
Example : The rate of a reaction triples when temperature changes from 20oC to 50oC. Calculate energy of activation for the reaction (R = 8.314 JK-1 mol-1). Solution: The Arrhenius equation is log10 k2/k1 = Ea/(R×2.303) [(T2-T1)/(T1 T2 )] Given: k2/k1 = 3; R=8.314 JK-1 mol–1; T1 = 20 + 273 = 293 K and T2 = 50 + 273 = 323 K Subtracting the given values in the Arrhenius equation, log10 3 = Ea/(8.314×2.303) [(323-293)/(323×293)] Ea = (2.303 × 8.314×323 × 293×0.477)/30 = 28811.8 J mol-1 = 28.8118 kJ mol-1 Example : In Arrhenius equation for a certain reaction, the value of A and Ea(activation energy) are 5×1013 sec-1 and 98.6 kJ mol-1 respectively. At what temperature, the reaction will have specific rate constant 1.1 × 10-3 sec-1 ? Solution : According to Arrhenius equation k = Ae-Ea/RT or loge k = loge A - Ea/RT loge e or 2.303 log10 k = 2.303 log10 A - Ea/RT or 2.303 log (1.1×10-3) = 2.303 log(4×1013)-(98.6×103)/(8.314×T) T = (98.6×103)/(8.314×2.303×16.56) K = 310.96 K Example : The rate constant is given by Arrhenius equation k = Ae-Ea/RT Calculate the ratio of the catalyst and uncatalysed rate constants at 25oC if the energy of activation of a catalysed reaction is 162 kJ and for the uncatalysed reaction the value is 350 kJ. Solution : Let kca and kun be the rate constants for catalysed and uncatalysed reactions. 2.303 log10 kca = 2.303 log10 A - (162×103)/RT .... (i) and 2.303 log10 kun = 2.303 log10 A - (350 × 103)/RT .... (ii) Subtracting Eq. (ii) from Eq. (i) log10 kca/kun = 103/(2.303 RT) (350-162) = (188× 103)/(2.303×8..314×298) = 32.95 kca/kun = 8.88 × 1032 |

Question 1:
Which of the following factors does not affect rate of a reaction ?
a. Temperature
b. Catalyst
c. Concentration of reactants
d. Nature of Product
Question 2:
Among the solids, rate increases with decrease in particle size.
a. pressure
b. particle size
c. concentration
d. mass of particle
Question 3:
A negative catalyst increases
a. rate of reaction
b. activation energy
c. amount of product formed
d. rate of backward reaction
Question 4:
The slope of plot log10 k vs [1/T] gives activation energy and intercept gives frequency factor
a.frequency factor
b. rate constant
c.rate f reaction

| Q.1 | Q.2 | Q.3 | Q.4 |
| d | b | b | a |
Related Resources
-
Click here for the detailed Syllabus of IIT JEE
-
Look here for Useful Books of Chemistry for IIT JEE
-
You can also refer to Introduction to chemical kinetics
To read more, Buy study materials of Chemical Kinetics comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Chemistry here.

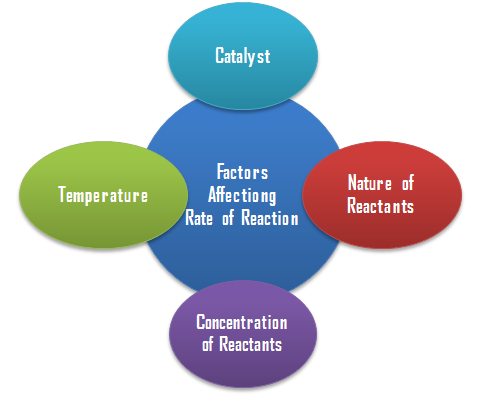



 fraction of the total number of collision which is effective.
fraction of the total number of collision which is effective.![On plotting log10 k against [1/T] we get a straight line On plotting log10 k against [1/T] we get a straight line](https://files.askiitians.com/cdn1/images/201495-111535328-6897-capture.png)
![log\frac{k_2}{k_1} =\frac{E_a}{2.303R}[\frac{1}{T_1}-\frac{1}{T_2}]](https://files.askiitians.com/cdn1/cms-content/common/latex.codecogs.comgif.latexlog_frack_2k_1_frace_a2.303r_frac1t_1-_frac1t_2.jpg)