Motion in Two Dimensions

 

Table of Content

Frame of Reference Choice of a Frame of Reference Motion in Two Dimensions Relative Motion Related Resources

In this part, we discuss motions in two dimensions like the motion of a particle moving on a circular path or on a parabolic path.

Consider a particle moving on x-y plane along a curved pat at time t, as shown in figure given below. Its displacement from origin is measured by vector  its velocity is indicated by vector  (tangent to the path of the particle) and acceleration 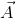 as shown in the figure.

The vectors ,  and 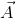 are inter related and can be expressed in terms of their components, using unit vector notation as,

From the above relations we can say that two-dimensional motion is nothing but superimpose of two one dimension motions. This is for the reason that in any two-dimensional motion, all the parameters can be resolved in two mutually perpendicular directions.

Frame of Reference

A frame of reference is a set of coordinate axes which is fixed with respect to a space point (a body or n object can also be treated as a point mass and therefore it can become a site for fixing a reference frame), which we have arbitrarily chosen as per our observer requirement. It is constituted of two components:

(i) Body on which observer is apparently sitting to observe the motion, i.e. the origin.

(ii) A coordinate system fixed on this body so that whatever is being observed can be measured or mathematically determined with the help of the coordinates of space points, which are defined by a unique set of (x, y, z). To fix a frame of reference one has to fix the origin to a chosen space point and then fix the co-ordinate system on it. Once the origin and coordinate system are fixed, then we have done the exercise of fixing the frame of reference and we can proceed to solve problems and study various parameters i.e. position, velocity, accelerations as functions o time.

Here, an important thing to notice is that earth becomes a natural choice for the frame of reference as in most of the cases it is very easy to visualize the motion with respect to it. As it is a routine in our daily life we innocently (even in early childhood) refer and perceive all motion phenomenon with respect to earth only.

While analyzing any motion we will take the help of the coordinate system. What we shall do is that we shall keep ourselves free to take it there. This is called a frame of reference because we shall refer to all positions in this coordinate system fixed on that body. Here, remembers that we fix all three axis of coordinate system i.e. 
X-axis. Y-axis and Z-axis as well as the origin on the body and the coordinates of origin are (0, 0, 0). It is the origin where we mostly assume that the observer is sitting to observe the motion in the concerned reference frame.

Choice of a Frame of Reference

Let us come back to the concept of motion. Do you believe that all what you see moving is in motion and what you see not moving is at rest! Like vehicles on road! You should be warned that motion or observation of motion is really not that simple!

Let us take an example: The moon in the night sky! Some time at night you see that moon is travelling across the clouds towards east or west. And in some other nights it doesn't move at all! We shall all agree that it cannot be. It cannot sometimes move faster and sometime slower and sometimes become stationary. Then, what is the phenomenon there?

Motion in Two Dimensions

We start with the first point that whenever we speak of any motion it should be with respect to some fixed frame of reference. So, when we see the moon moving. It is not with certainly one can point out that in the night when it looked stationary there were no clouds. So it is an effect of the clouds. The fact is that if we have clouds in some nights moving towards west or east then we see moon travelling towards east or west in the sky respectively. How to explain it with the help of reference frames? It is like this. When we see two objects in the sky one moon and other a cloud, then due to relatively bigger size of clouds (as seen by us) one gets his eyes fixed on clouds and therefore frame of reference gets fixed on the clouds (Figure shown above). It is equivalent to say that we are sitting on the clouds itself, which looks stationary to us and the feeling comes, as if moon is travelling across this stationary cloud in the opposite direction to the clods motion (see figure given above). Similarly, we see things going backwards when we travel on a road.

Now let us deliberately fix our eyes on the moon and see. What we are doing now is that we are fixing frame of reference on the moon. It is equivalent to say that we are sitting on the moon to observe the cloud's motion and now we can see clouds drifting away (which is the fact). See Figure shown above.

An important observation to remember is that once we choose an object as a frame of reference, we can't see it moving with respect to itself. Naturally, in most of the cases of observations the Earth becomes a natural choice for the reference frame. Also, based on the choice of reference frames one can have many apparent motion of an object under consideration.

Here one important point to be noted is that in all previous discussion we have assumed that the reference frames are not accelerating, which means it's acceleration is zero. These are called inertial or un accelerated frames of reference. Now obviously, we are left with one more choice of class of reference frames that is the accelerated ones. These are called 
non-inertial or accelerated frame of reference. But in all the forthcoming exercises in this chapter we shall deal with and look only for inertial frames of reference.

Relative Motion

Consider a observer S is fixed to the earth. The other observer S' is moving on the earth, say a passenger sitting on a bus. Hence other frame of reference S' is fixed with bus. Each observer is studying the motion of a cyclist in his or her own frame of reference. Each observer will record a displacement, velocity and acceleration for the cyclist measured relative to his reference frame. Now the question is "How will we compare their results"?. To do this we need the concept of relative motion. Let us do it.

In figure shown above at the top, the reference frame S, represented by the x and y-axes, can be thought of as fixed to the earth. The other reference frame S', represented by x'- and y'-axes, which moves along the x-axis with a constant velocity u, measured in the s-system, fixed with the bus.

Initially, a particle is at a point called A in the S-frame and called A' in the S'-frame. At a time t later, the reference frame S' has moved a distance ut to the right and particle has moved to B. The displacement of the particle from its position in the S-frame is the vector  from A to B. The displacement of the particle from its initial position in the S'-frame is the vector r' from A' to B. These are different vectors because the reference point A' of the moving frame has been displaced a distance ut along the x-axis during the motion. From the second figure shown above we see that  is the vector sum of  and :

 = +

Differentiating equation leads to

But,

  

is  the instantaneous velocity of the particle measured in the s-frame.

 and

is the instantaneous velocity of the same particle measured in the S' frame, so that

  = ' + .................. [A]

Hence the velocity of the particle relative to the S-frame,  is the vector sum of the velocity of the particle to the S' frame, , and the velocity  of the S' frame relative to the S-frame.

Once again differentiating equation [A]

 We get,

Hence the acceleration of particle is the same in all reference frame moving relative to one another with constant velocity

Problem 1:-

A particle starts with initial velocity (3i + 4j) m/s and with constant acceleration (8i + 6j) m/s². Find the final velocity and final displacement of the particle after time t = 4 sec.

Solution:-

As the velocity and acceleration vectors are not parallel, the velocity and acceleration cannot be treated as a scalar.

Now divide the whole phenomenon in two one-dimension motions.

In x-direction,

Initial velocity = v_x0 = 3m/s, a_x = 8 m/s²

Hence velocity after 4 second, v_x = 3 + 8 × 4 = 35 m/s

Displacement after 4 second s_x = x = 3 × 4 + ½8 (4)² = 76 m

In y-direction,

Initial velocity v_y0 = 4m/s, a_y = 6 m/s²

Velocity after 4 second v_y = 4 + 6 × 4 = 28 m/s

Displacement after 4 second s_y = 4 × 4 + ½ 6 (4)² = 64 m

It means final velocity v = v_x i + v_y j = (35 i + 28 j) m/s 

and displacement = s s_x i + s_y j = (76 i + 64 j) m 

Problem 2:-

There are two boats B₁ and B₂. They are continuously moving towards a bank. Water flow velocity is 10m/sec away from the bank. When at one instant of time, observation was taken we found that B₁ and b₂ are at a position (figure is gen below) which is 100 m from the bank and after 1 sec, b₁ is 50 away and B₂ is 25m away from the bank. Find out all possible (motion) velocities observed from different reference frames choices.

Solution:-

Here we have four (at least) immediate choices of reference frames with respect to which we can observe velocities.

(i)     Bank (earth)

(ii)    B₁

(iii)    B₂

(iv)   Water

(i) Bank:   (See figure shown above) First we shall fix the frame of reference on the bank.

Since B₁ travels 50 m towards the bank in 1 sec., its velocity towards the Bank (that is in +y direction) is 50m/sec.

Similarly B₂ travels 75 m/s towards the bank

Thus, its velocity with respect to bank or as observed by an observer sitting at rest on the bank is

75m/sec (+y direction)

Since water moves away from bank at speed of 10m/sec.

Therefore, water's velocity w.r.t. the bank is 10m/sec (-y direction).

(ii) Boat B1:   Now, let us fix frame of reference on Boat B₁.

See the right side figure:

(a) Since B₁ cannot move w.r.t. itself (only in case of deformation, a part of this boat can be seen moving w.r.t. other parts)

 Thus, V_B1 = 0 (relative velocity w.r.t. to itself)

(b) at t = 0, B₁ and B₂ were in the same line and had no

at t = 1 B₂ leads B₁ by 25 m

that is B₂ has moved 25m in 1 sec w.r.t. B₁

Thus, V_B2 = 25 m/sec (+ direction)

(c)   Bank, at t = 0 was away by 100 m.

and at t = 1 it has come closer by 50 m towards B₁

Therefore, bank is approaching B₁ by a speed of

V_bank = 50m/sec (-y direction)

(d)   To visualize the motion of water w.r.t. B₁ we can imagine a wooden piece of negligible mass, floating on the water surface. Its velocity will be equal to that of water. At t = 0 the piece was in the same line joining B₁ and B₂ at a distance of 100 m from the bank.

At t = 1 sec it will move away by 10m from the bank that is its distance from b₁ will be 60m (see figure shown above)

Following a similar approach find out various relative velocities as seen from frames of reference, which are fixed, on boat B₂ (figure shown below) and when the reference frame is fixed on water. (Figure shown next after this given below)

Problem 3:-

A windblown rain is filling, 20 degrees from the vertical, at 5 m/s. Passengers in a car see the rain falling vertically. What is the magnitude and direction of car's velocity?

Solution:-

Here we have two frames S and S'. Frame S is attached with ground while S' attached with car. To determine the magnitude and directions of car's velocity, we use the concept of relative motion discussed earlier.

Let v_RG = velocity of rain with respect to ground

v_RC= velocity of rain with respect to car

v_c= velocity of car with respect to ground

From the equation for relative velocity in two frames, we get

From the vector diagram we see that car should be travelling along the inclined direction of rain with velocity

v_C = 5 sin 20^o m/s

Question 1:-

For a body, moving along a straight line, the average velocity is equal to its instantaneous velocity. The motion of the body should be:

(a) uniform                                     (b) uniformly accelerated

(c) non-uniformly accelerated          (d) may be uniform or non-uniform

Question 2:-

A toy car is moving in a circular track covering equal distances in equal intervals of time. This shows that the toy car is moving with:

(a) uniform velocity                      (b) varying speed

(c) uniformly acceleration             (d) uniform speed and acceleration of fixed magnitude

Question 3:-

A bomb is released by a horizontal flying aeroplane. The trajectory of the bomb is:

(a) straight line           (b) circle        (c) hyperbola          (d) parabola

Question 4:-

A body is dropped from a height of 490 m from the ground. It will hit the ground after:

(a) 10 s      (b) 20 s     (c) 30 s      (d) 33 s

Q.1	Q.2	Q.3	Q.4
a	d	d	a

 

Related Resources

• You might like to refer Motion in a Vertical Circle.

• For getting an idea of the type of questions asked, refer the  Previous Year Question Papers.

• Click here to refer the most Useful Books of Physics.

To read more, Buy study materials of Kinematics comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Physics here.