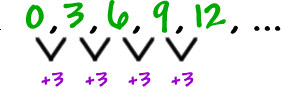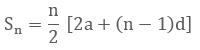Introduction of Sequences and Series
Table of contents |
|
|
Meaning of Sequence
A sequence is a group of objects which follow some particular pattern. If we have some objects listed in some order so that it has 1st term, 2nd term and so on, then it is a sequence.
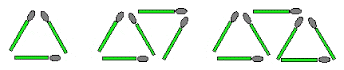
In this image we can see the group of sticks with a certain pattern, so we can observe that what could come next
As we can see that the next figure in the sequence will have 9 sticks.
What is a sequence in Math?
In Mathematics, it is a group of numbers in an ordered form which follow a certain pattern is called Sequence.
These numbers are called ‘Term’ or ‘Members’ or ‘Elements’. It is similar as a set of numbers.
As in the above figure 5,8,11,14,17 are the terms of the sequence.
Finite Sequence
The sequence which have limited or finite number of terms is called Finite Sequence.
Example
{1, 3, 9, 27} is the sequence of multiples of 3.
{m, o, n, k, e, y} is the sequence of letters in the word "monkey".
Infinite Sequence
The sequence which have unlimited or infinite number of terms or it has no end is called Infinite Sequence.
Example
This is the infinite sequence of even numbers. It is the three dots here which shows that it is an infinite sequence, with no end. So its last term will be represented by n∞.
In the other way we can write it as
Here ∞ the infinity means infinite sequence.
Types of Sequence
There are three types of sequence
-
Arithmetic Sequence
-
Geometric Sequence
-
Fibonacci Sequence
Arithmetic Sequence
Any sequence in which the difference between every successive terms is constant then it is called Arithmetic Sequence. It could be in ascending or descending form according to the constant number.
Example
Here we are getting the terms by adding 3 every time. this is the difference between the two successive terms so it is called the difference.
The difference is represented by “d”.
In the above example we can see that a1 =0 and a2 = 3.
The difference between the two successive terms is
a2 – a1 = 3
a3 – a2 = 3
If the first term of an arithmetic sequence is a1 and the common difference is d, then the nth term of the sequence is given by:
an = a1+ (n−1) d
Geometric Sequence
Any sequence in which the ratio between every successive terms is constant then it is called Geometric Sequence. It could be in ascending or descending form according to the constant ratio.
Example
Here
a1 =1
a3 = 16 = a2(4)
Here we are multiplying it with 4 every time to get the next term. Here the ratio is 4 .
The ratio is denoted by “r”.
an = an−1⋅r or an = a1⋅rn−1
Fibonacci Sequence
By adding the value of the two terms before the required term, we will get the next term. Such type of sequence is called Fibonacci sequence. There is no visible pattern.
Example
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ...
In the above sequence, we can see
a1 =0 and a2 = 1
a4 = a3 + a2 = 1 + 1 =2 and so on.
So the formula of the Fibonacci Sequence is
an = an – 2 + an – 1, n > 2
This is also called the Recursive Formula.
Meaning of Series
The summation of all the numbers of the sequence is called Series. Generally it is written as Sn.
Example
If we have a sequence 1, 4, 7, 10, …
Then the series of this sequence is 1 + 4 + 7 + 10 +…
Notation of Series
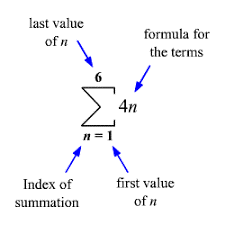
We use the sigma notation that is, the Greek symbol “Σ” for the series which means “sum up”.
The series 4 + 8 + 12 + 16 + 20 + 24 can be expressed as ∑6n = 1 4n. We read this expression as the sum of 4n as n goes from 1 to 6.
Finite and Infinite Series
A series with finite number of terms is called Finite Series.
A series infinite number of terms is called Infinite Series.
2 + 4 + 6 + 8 + 10 + …
Types of Series
There are different types of series-
Arithmetic Series
Arithmetic series is the summation of the terms of the arithmetic sequence that is, if the difference between the every term to its preceding term is always constant then it is said to be an
The arithmetic series is in the form of
{a + (a + d) + (a + 2d) + (a + 3d) + .........}
where a is the first term of the series and d is the difference of it which is known as the common difference of the given series.
Formula of Arithmetic Series
If a is the first term, d is the difference and n is the total number of the terms, then the formula for nth term is given by
an = a + (n - 1) d
Sum of an Arithmetic Series
Geometric Series
Geometric series is the summation of the terms of the geometric sequence i.e. if the ratio between the every term to its preceding term is always constant then it is said to be a geometric series.
Formula of Geometric Series
In general, we can define geometric series as
Where, a is the first term of the series and r is the common ratio for it.
Formula for nth term of the geometric series
an = a1 r n - 1
Where, n is the number of the term.
Meaning of Arithmetic Progression (A.P.)
Arithmetic Progression is the sequence of numbers such that the difference between the two successive terms is always constant. And that difference is called the common difference. It is also known as Arithmetic Sequence.
Meaning of Geometric Progression (G.P.)
Geometric Progression is the sequence of numbers such that the next term of the sequence comes by multiplying or dividing the preceding number with the constant (non-zero) number. And that constant number is called the Common Ratio. It is also known as Geometric Sequence.
a, ar, ar2, ar3, …, arn
Arithmetic Mean
Arithmetic mean is basically the average of two numbers. If we have two numbers n and m, then we can include a number L in between these numbers so that the three numbers will form an arithmetic sequence like n, L, m.
In that case the number L is the arithmetic mean of the numbers n and m.
According to the property of Arithmetic progression, we can say that-
L – n = m – L that is, the common difference of the given AP.
This is generally used to find the missing number of the sequence between the two given numbers.
Example
What will be the 6th number of the sequence if the 5th term is 12 and the 7th term is 24?
As the two numbers are given so the 6th number will be the Arithmetic mean of the two given numbers.
Hence the 6th term will be 18.
Geometric Mean
Geometric Mean is the Special type of average of two numbers. If a and b are the two numbers then the geometric mean will be
Example
Find the geometric mean of 2 and 18.
Solution:
We can use the above formula to calculate the geometric mean.
a = 2 and b = 18
Relation between A.M. and G.M.
Here we can see that the sequence 2, 6, 18 is a geometric progression.
As we have seen above the formula for the Arithmetic mean and the Geometric mean are as follows:
where a and b are the two given positive numbers.
Let A and G be A.M. and G.M.
So
Now let’s subtract the two means with each other
This shows that A ≥ G
Example
Find the two numbers, If Arithmetic mean and Geometric mean of two positive real numbers are 20 and 16, respectively.
Solution:
Given
Now we will put these values of a and b in
(a – b)2 = (a + b)2 – 4ab
(a – b)2 = (40)2 – 4(256)
= 1600 – 1024
= 576
a – b = ± 24 ( by taking the square root) …(3)
By solving (1) and (3), we get
a + b = 40
a – b = 24
a = 8, b = 32 or a = 32, b = 8
Special Series
Special Series are the series which are special in some way. It could be arithmetic or geometric.
Some of the special series are:
(i) 1 + 2 + 3 +… + n (sum of first n natural numbers)
(ii) 12 + 22 + 32 +… + n2(sum of squares of the first n natural numbers)
(iii) 13 + 23 + 33 +… + n3(sum of cubes of the first n natural numbers).
Sum to n terms of Special Series
More Readings