Solution of Triangles
In a triangle ABC, the vertices and the angles are denoted by capital letters and the sides by small letters.
In the figure given below, the sides opposite to angles A, B, C are denoted by a, b, c respectively. The area of the triangle is denoted by S or Δ.

Basic Formulae and Results:
Some of the basic trigonometry formulae depicting the relationship between the sides and angles of a triangle are listed below:
Sine rule
This rule states that the sides of any triangle are proportional to the sines of the angle opposite to them in ?ABC, i.e.
a/ sin A = b/ sin B = c/ sin C
Note:
-
The rule can further be expressed as (sin A)/a = (sin B)/b = (sin C)/c
-
The rule is extremely useful for expressing the sides of a triangle in terms of sines of angle or vice versa as per the requirement of the question. Hence, for the form a/ sin A = b/ sin B = c/ sin C = k, we have,
a = k sin A, b = k sin B, c = k sin C
and for (sin A)/a = (sin B)/b = (sin C)/c = l, we have
sin A = la, sin B = lb, sin C = lc
Cosine rule
In any triangle ABC, the following results hold good:
cos A = (b2 + c2 - a2 )/2ac
cos B = (a2 + c2 - b2)/2ac
cos C = (a2 + b2 - c2)/2ab
Note: In case
-
∠A = 60°, then b2 + c2 - a2 = bc
-
∠B = 60°, then a2 + c2 - b2 = ac
-
∠C = 60°, then a2 + b2 - c2 = ab
Trigonometric ratios of half-angles:
-
sin A/2 = √(s-b) (s-c)/bc
-
sin B/2 = √(s-b) (s-c)/bc
-
sin C/2 = √(s-a) (s-b)/ab
-
cos A/2 = √s(s - a)/bc
-
cos B/2 = √s(s - b)/ca
-
cos C/2 = √s(s - c)/ab
-
tan A/2 = √(s - b) (s - c)/s(s - a)
-
tan B/2 = √(s - c) (s - a)/s(s - b)
-
tan C/2 = √(s - a) (s - b)/s(s - c)
Projection rule:
-
a = b cosC + c cosB
-
b = c cosA + a cosC
-
c = a cosB + b cosA
Semi-perimeter of the triangle
If ‘s’ is assumed to be the perimeter of the triangle then s = a + b + c / 2
Area of a triangle
If Δ is the area of the triangle ABC then
-
Δ = 1/2 bc sin A = 1/2 ca sin B = 1/2 ab sin C
-
Δ = √s(s - a) (s - b) (s - c), this is also called as the Hero’s Formula
-
Δ = (a2 sin B sin C)/ 2 sin (B + C) = (b2 sin C sin A)/ 2 sin (A + C) = (c2 sin A sin B)/ 2 sin (A + B)
Some illustrations based on these formulae
Illustration:
Find out the length of x in the figure given below
Solution:
Whenever we need to find the length of a side, a different sort of sine formula is used which simplifies the calculation of length:
Using the result, a/sin A = b/ sin B
Here, a = 7, b = x, A = 60°, B = 80°
7/ sin (60°)) = x / sin (80°)
Multiplying both sides by sin (80°) for simplification we get
(7/sin (60°)) sin (80°) = x
Hence, on simplification we get
x = 7.96, hence this is the required length.
Illustration:
Find the missing side in the diagram below:

Solution:
Here, we will have to apply the cosine formula.
a2 = b2 + c2 - 2bc cos A
Hence substituting the values we get,
h2 = 882 + 1462 – 2×88×146×cos 53°
h2 = 13595.761.
For more clarification, refer the video
Some vital trigonometry theorems associated with solution of triangles:
Napier’s analogy
In any triangle ABC, the following results hold good:
- tan (B – C)/2 = (b – c)/(b +c) cot A/2
- tan (C – A)/2 = (c –a)/(c + a) cot B/2
- tan (A – B)/2 = (a – b) /(a + b) cot c/2
m-n theorem
If D be the point on the side BC of a triangle ABC which divides the side BC in the ratio m: n, then with respect to the figure given below, we have:
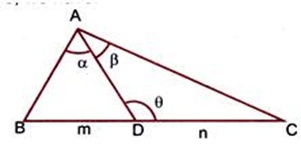
(m + n) cot θ = m cot α – n cot ß.
(m + n) cot θ = n cot B – m cot C.
Apollonius theorem
Consider a triangle ABC. As depicted in the figure given below, D is the median through A.
Then AB2 + AC2 = 2(AD2 + BD2).
Process of Solution of Triangles:
A triangle is known completely if the three sides and angles are known. These constitute the elements of the triangle. Thus, if we have any three elements of a triangle (other than the three sides) say two sides and the included angle or alike then we can easily find the rest of the elements using the various formulae. Hence the triangle is known completely and this process is called the solution of triangles.
We list below the various ways of preceding a given problem when some elements are unknown:
-
If the three sides a, b, c are given, angle A is obtained from
tan A/2 = √(s - b) (s - c)/s(s - a) or cos A = b2 + c2 - a2 / 2bc.
B and C can be obtained in the similar way.
The cosine formula should be used only when a, b and c are small numbers.
-
If two sides b and c and the included angle A are given, then
tan (B – C)/2 = (b – c)/ (b + c) cot A/2 gives (B – C)/2.
Also B + C/2 = 90o - A/2, so that B and C can be evaluated. The third side is given by a = b sin A/sin B or a2 = b2 + c2 – 2bc cos A.
-
If two sides b and c and the angle B (opposite to side b) are given, then sin C = c/b sin B, A = 180o – (B + C) and b = b sin A/sin B give the remaining elements.
If b < c sin B, there is no triangle possible (Fig. 1)
If b = c sin B and B is an acute angle, then only one triangle is possible (Fig. 2)
If c sin B < b < c and B is an acute angle, then there are two values of angle C (Fig. 3).
If c < b and B is an acute angle, then there is only one triangle (Fig. 4).
This is, sometimes, called an ambiguous case.
Alternative Method:
By applying cosine rule, we have cos B = a2 + c2 - b2/2ac
⇒ a2 – (2c cos B) a + (c2 – b2) = 0
⇒ a = c cos B + √(C cos B)2 - (c2 - b2)
⇒ a = c cos B + √b2 - (c sin B)2.
This equation leads to the following cases:
Case –I
If b < c sin B, no triangle is possible.
Case –II
Let b = c sin B. There are further the following cases:
(a) B is an obtuse angle
⇒ cos B is negative. There exists no such triangle.
(b) B is an acute angle
⇒ cos B is positive. There exists only one triangle.
Case –III
Let b < c sin B. We have the following cases:
-
B is an acute angle ⇒ cos B is positive. In this case two values exist if and only if c cos B > √b2 - (c sin B)2 or
c > b ⇒ Two triangles are possible.
If c < b, only one triangle is possible.
-
B is an obtuse angle ⇒ cos B is negative. In this case triangle will exist if and only if √b2 - (c sin B)2 > c cos B ⇒ b > c. So in this case only one triangle is possible.
If b < c there exists no triangle.
If one side a and angles B and C are given, then A = 180o – (B + C), and b = a sin B/sin A, c = a sin C/sin A .
If the three angles A, B, C are given, we can only find the ratios of the sides a, b, c by using the sine rule (since there are infinite similar triangles possible).
You might like to refer some of the related resources listed below:
-
Look into the Revision Notes on Solution of Triangles for a quick revision.
-
Various Recommended Books of Mathematics are just a click away.
View courses by askIITians


Design classes One-on-One in your own way with Top IITians/Medical Professionals
Click Here Know More

Complete Self Study Package designed by Industry Leading Experts
Click Here Know More

Live 1-1 coding classes to unleash the Creator in your Child
Click Here Know More

a Complete All-in-One Study package Fully Loaded inside a Tablet!
Click Here Know MoreAsk a Doubt
Get your questions answered by the expert for free


