Critical Angle Formula

 

Table of Content

Total Internal Reflection Applications Test your knowledge Related Resources

 

Total Internal Reflection 

When a ray of light AO passes from an optically denser medium to a rarer medium, at the interface XY, it is partly reflected back into the same medium along OB and partly refracted into the rarer medium along OC as shown in figure.

If the angle of incidence is gradually increased, the angle of refraction r will also gradually increase and at a certain stage r becomes 90^o. Now the refracted ray OC is bent so much away from the normal and it grazes the surface of separation of two media. The angle of incidence in the denser medium at which the refracted ray just grazes the surface of separation is called the critical angle c of the denser medium.

If i is increased further, refraction is not possible and the incident ray is totally reflected into the same medium itself. This is called total internal reflection.

 

If µ_d is the refractive index of the denser medium then, from Snell’s Law, the refractive index of air with respect to the denser medium is given by,

µ_a/ µ_d = sin i /sin r

1/ µ_d = sin i/sin r       (Since, µ_a = 1 for air)

If r = 90^o, i = c

sin c/sin 90^o = 1/µ_d 

Or, sin c = 1/µ_d

Or, c = sin^-1(1/µ_d)

If the denser medium is glass, c = sin^-1(1/µ_g)

Hence for total internal reflection to take place (i) light must travel from a denser medium to a rarer medium and (ii) the angle of incidence inside the denser medium must be greater than the critical angle i.e. i > c.

Table: Critical angle for some media

Medium	Refractive index	Critical  angle
Water	1.33	48.75o
Crown glass	1.52	41.14o
Dense flint glass	1.62	37.31o
Diamond	2.42	24.41o

Watch this Video for more reference
 

Applications

(i) Diamond

Total internal reflection is the main cause of the brilliance of diamonds. The refractive index of diamond with respect to air is 2.42. Its critical angle is 24.41^o. When light enters diamond from any face at an angle greater than 24.41^o it undergoes total internal reflection. By cutting the diamond suitably, multiple internal reflections can be made to occur.

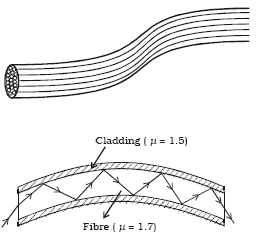
(ii) Optical fibres

The total internal reflection is the basic principle of optical fibre. An optical fibre is a very thin fibre made of glass or quartz having radius of the order of micrometer (10^–6m). A bundle, of such thin fibres forms a ‘light pipe’ as shown in figure.

Figure shows the principle of light transmission inside  an  optical  fibre.  The refractive index of the material of the core is higher than that of the cladding. When the light is incident at one end of the fibre at a small angle, the light passes inside, undergoes repeated total internal reflections along the fibre and finally comes out. The angle of incidence is always larger than the critical angle of the core material with respect to its cladding. Even if the fibre is bent or twisted, the light can easily travel through the fibre.

Light pipes are used in medical and optical examination. They are also used to transmit communication signals.

Total internal reflection takes place when a light ray is in the denser medium and approaching the less dense medium. Total internal reflection takes place when the angle of incidence for the light ray is greater than the so-called critical angle. The critical angle is defined as the angle of incidence that provides an angle of refraction of 90-degrees. The critical angle can be calculated by taking the inverse-sine of the ratio of the indices of refraction.  The critical angle can be used to predict the critical angle for any boundary, provided that the indices of refraction of the two materials on each side of the boundary are known.  At any angle greater than the critical angle, total internal reflection occurs and the light ray obeys the normal rules for reflection (i.e. angle of incidence = angle of reflection). The critical angle is only defined when n2/n1 is less than 1. If light is incident on an optical fiber with an angle of incidence greater than the critical angle then the light will remain trapped inside the glass strand. Light can travel over a very long distance without a significant loss. As the angle of incidence increases, the angle of refraction increases. This phenomenon helps in understanding the movement of light in optical fibers. Monolithic ring resonators can be fabricated where total internal reflection occurs at all or some of the interfaces. It is also used in slab lasers. It helps one to understand a zig-zag path through the medium.

Problem (JEE Main):

Critical angle of glass is θ₁ and that of water is θ₂. The critical angle for water and glass surface would be (µ_g = 3/2, µ_w = 4/3)

(a) less than θ₂          (b) between  θ₁ and θ₂.

(c) greater than θ₂      (d) less than θ₁

Solution:

sin θ₁ = 1/µ_g    and sin θ₂ = 1/µ_w

Since, µ_g > µ_w, θ₁ < θ₂

Critical angle θ between glass and water will be given by

sin θ = µ_w/µ_g

Or θ > θ₂

Thus from the above observation we conclude that, option (c) is correct.

 

Due to total internal reflection an underwater swimmer looking up at the surface of the water from a depth of 10 ft sees a mirrored surface with a hole in it of radius R.  Find R if the index of refraction of water is 1.33.

(a) 5.67 ft,  (b) 7.46 ft,  (c) 9.12 ft,  (d) 11.3 ft,  (e) none of them

Question 2

In the reflection of light flat and smooth surface

(a) the angle of incidence equal the angle of reflection

(b) the angle of incidence is larger than the angle of reflection

(c) the angle of incidence is smaller than the angle of reflection

(d)  none of the above

Question 3

The following are true about total internal reflection:

(a) it occurs when the incident ray exceeds the critical angle

(b) it isn't  used in binoculars

(c) it occur when light travel from a medium with lower refractive

index to one with higher index.

(d) have all of the properties listed above.
 

Question 4

Light is confined within the core of a simple optical fiber by

(a) refraction

(b) total internal reflection at the outer edge of the cladding.

(c)  total internal reflection at the core cladding boundary

(d) reflection from the fiber's plastic coating

Question 5

When total internal reflection occurs...

(a) the angle of incidence is greater than 90°.

(b) the angle of incidence is greater than the angle of refraction.

(c) the angle of refraction is greater than 90°.

(d) the angle of incidence is equal to 90°.

Question 6

For which of the following cases will the total internal reflection of light be possible?

(a) Angle of incidence is less than the critical angle.

(b) Angle of incidence is equal to the critical angle.

(c) Angle of incidence is greater than the critical angle.

(d) Angle of incidence is equal to the angle of refraction.

Q.1	Q.2	Q.3	Q.4	Q.5	Q.6
d	a	a	c	c	c

Related Resources

• You might like to iit jee ray optics study material.

• For getting an idea of the type of questions asked, refer the  Previous Year Question Papers.

• Click here to refer the most Useful Books of Physics.

• To get answer to any question related to critical angle and total internal reflection click here.

To read more, Buy study materials of Ray Optics and Optical Instruments comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Physics here.