Refraction through a Prism
Table of contents |
Refraction through a Glass Slab and Glass Prism
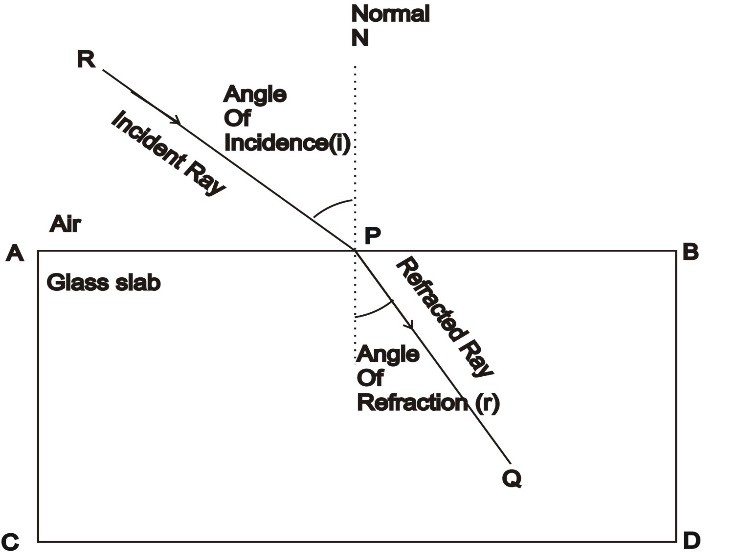
Let us consider a rectangular glass slab ABCD. When a light ray RQ after travelling through air, is incident on the glass slab at a point P the light gets refracted. Since the glass slab is a denser medium compared to air, thus the ray gets bend towards the normal. The difference between glass slab and glass prism is that the opposite faces of a rectangular glass slab is parallel while the opposite faces of prism is not parallel to each other.
Glass Prism
Let us consider a triangle prism as shown in the figure given below. It consists of three rectangular faces and two triangular ends. We have learnt that the opposite faces of a triangular prism is not parallel to each other. In the diagram given below, M1 and M2 are the two faces of the prism where the refraction of light takes place. They are inclined to each other at an angle known as the Angle of Prism.
Here ∠AOC is the angle of prism. The ray diagram of a glass prism resembles to that of a triangle. A glass prism is also sometimes referred to as only prism. Refraction that takes place in glass slab is different from that of the prism in the sense that the emergent ray in a glass slab is parallel to the incident ray whereas the emergent ray in a glass prism is not parallel to the incident ray. It is deviated from its original path by a certain angle. Let us now study in detail how refraction takes place in a glass prism.
Refraction through a Glass Prism
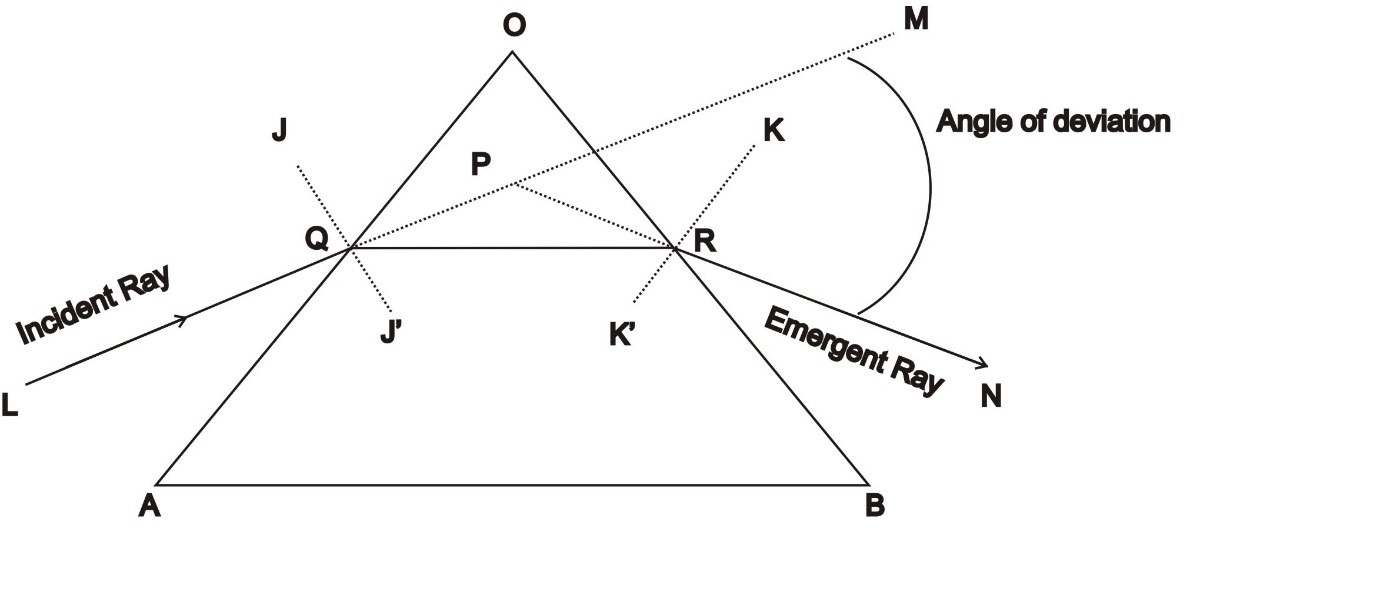
When a light ray is allowed to pass through a glass prism, it gets refracted twice. First, at the entrance of the prism and second when the light exits from the prism. Here the two refracting surface i.e. AO and BO are not parallel to each other. Thus the incident ray is not parallel to the emergent ray. As it can be seen from the diagram given below a glass prism AOB is made to stand on its base AB. Here the line JJ’ and KK’ are normal to the surfaces AO and BO respectively. LM is the incident light that is made to fall on the surface of prism that is, AO. As the light ray is travelling from rarer medium to the denser medium the light ray bends towards the normal QJ’ and follows the path QR inside the prism. QR is the refracted ray of light which bends towards the base of prism AB. Now the refracted ray QR after travelling through the prism, exits the prism at point R. At this point the ray is again refracted. Now since the refracted ray QR is travelling from denser to rarer medium (glass to air) it bends away from the normal KR and traverses the path RN. This ray is known as Emergent Ray. In this case also we can see that the emergent ray bends towards the base of the prism.
Thus we can conclude that when a ray of light travels through a prism, it always tends to bend towards the thicker part of the prism.
As we already know that both the surfaces of the prism are not parallel to each other, therefore the emergent ray RN and incident ray QL are also not parallel to each other. Now let us extend the incident ray QL to a point M. This extended line is the original direction of the incident ray. Thus we can define angle of deviation as the angle between the original path of the incident ray and the emergent ray.
Refractive Index of a Prism
Now let us consider the prism given above. In the quadrilateral PBDC, at the vertices B and C, two of the angles are right angles. Therefore,
∠P + ∠BDC = 180° ………… (1)
In ∆ BDC,
r1 + r2 + ∠BDC = 180°……….. (2)
r1 + r2 = P …….. (3)
Now, we can define the total deviation ∅ as the sum of deviation at the two surfaces.
∅ = (i - r1) + ( e - r2)
∅ = i + e – A ………….. (4)
Thus we can conclude that angle of deviation depends on the angle of incidence.
When the deviation is minimum, the refracted ray becomes parallel to the base of the prism. Let Dmin denote minimum deviation which is equal to angle of deviation ∅. In the case of minimum deviation, angle of incidence (i) is equal to the angle of refraction that is, i = e and r1 = r2.
From equation (3),
2r = P
r = P/2
Similarly,
The refractive index(µ) of the prism is given by,
Equation (5) helps us to determine the refractive index of the prism. For a prism, whose angle is negligible, Dmin is also very small.
Frequently Asked questions (FAQs)
Q1. What is meant by dispersion of light?
Sol. Dispersion of light can be defined as a process where a white light when allowed to pass through a triangular prism is separated into seven different component of colors. The seven different colors are Violet, Indigo, Blue, Green, Yellow, Orange, and Red. The seven different colors are also sometimes abbreviated as VIBGYOR.
Q2. What is the cause of dispersion of white light?
Sol. When a ray of white light passes through a prism, it suffers refraction twice which breaks the components of white light into seven different colors. Thus refraction is the only reason that could correctly explains the reason behind dispersion of light.
Q3. What does the prism do?
Basically, the main work of prism is to break a ray of light into its color components. Its finds application in astronomical telescope, spectroscope etc.
Watch this Video for more reference
More Readings