Calculations Involving Unit Cells Dimensions
Table of contents |
Calculations Involving Unit Cells Dimensions
With the help of geometry and attributes of unit cells, we can easily evaluate the volume of the unit cell. With volume and mass of atoms, we can also evaluate the density of the unit cell. A crystal lattice is represented in terms of unit cells; we can determine the density of crystal lattices by evaluating the density of unit cells.
Image 1: Volume of Unit Cell
Density of Unit Cell
A unit cell is a three-dimensional structure occupying one, two or more atoms. With the help of dimensions of unit cells, we can evaluate the density of the unit cell. To do so let’s consider a unit cell of edge length ‘a’, therefore the volume of the cell will be ‘a3’. Also, density is defined as the ratio of the mass of unit cell and volume of the unit cell.
So we can write
Mass of unit cell varies with number of atoms “n” and mass of a single atom “m”. Mathematically mass of unit cell is the product of number of atoms “n” and mass of one atom “m” i.e.
Mass of Unit Cell = n × m
Also from quantitative aspect of atoms, mass of one atom can be written in terms of Avogadro Number ( NA ) and molar mass of atom ( M), that is,
Volume of Unit Cell = a3
Placing the required values in equation 1 we get
Therefore if we know molar mass of atom “M”, number of atoms “n”, the edge length of unit cell “a” we can evaluate the density of unit cell.
Derived Results to Evaluate Density of Unit Cell
Following results can be used to derive density of unit cell:
Image 2: By knowing number of atoms we can easily determine volume of any type of unit cell
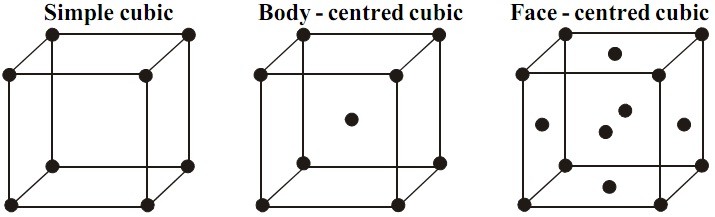
Simple or Primitive Unit Cell
Image 3: Simple Unit Cell
There is only one atom present in the simple or primitive unit cell. Therefore density of simple unit cell is
Body-centred Unit Cell
Image 4: Body-centred Unit Cell
The value of number of atoms ‘n’ is 2, so density of body-centred unit cell is
Face-centred Unit Cell
Image 5: Face-centred Unit Cell
Face-centred Unit Cell contains 4 atoms, therefore its density is
Example 1
The density of a face-centred unit cell is 6.23 g cm-3. Given the atomic mass of a single atom is 60, evaluate the edge length of the unit cell. (Take value of NA = 6.022 × 1023)
As the unit cell is a face-centred unit cell, a number of atoms will be 4. We have
n = 4 , M = 60 , NA = 6.022 × 1023 and d = 6.23 g cm-3
We know that
After evaluating we get the value of edge length of the cube to be 4 × 10-8 cm.
Example 2
KBr or potassium bromide has density 2.75 g cm-3. The edge length of its unit cell is 654 pm. Prove that KBr depicts face-centred cubic structure.
We have edge length of unit cell = 654 pm = 6.54 × 10-8 cm
Therefore volume of the cell = (6.54 ×10-8)3 cm3
Molar Mass of Potassium Bromide ( KBr) is 119 g/mol
Density of KBr = 2.75 g cm-3
We know that
Evaluating we get value of n to be 3.09 ≈ 4
Since a number of atoms is 4 we can clearly say that KBr is a face-centred cubic structure.
Watch this Video for more reference
More Readings