Packing Fractions

Table of Content

Simple Cubic Unit Cell
Body-centred Cubic Unit Cell
Face-Centred Cubic
Calculation Involving Unit Cell Dimensions
Related Resources

Packing faction or Packing efficiency is the percentage of total space filled by the particles.

Both hcp & ccp though different in form are equally efficient. They occupy the maximum possible space which is about 74% of the available volume. Hence they are called closest packing.
In addition to the above two types of arrangements a third type of arrangement found in metals is body centred cubic (bcc) in which space occupied is about 68%.
Packing Efficiency = $\frac{Volume\ occupied\ by\ all\ the\ spheres\ in \ unit\ cell}{Total\ volume\ of\ the\ unit\ cell}\times 100$

Let us calculate the packing efficiency in different types of structures

Simple Cubic Unit Cell

Let ‘a’ be the edge length of the unit cell and r be the radius of sphere.

As sphere are touching each other

Therefore a = 2r

No. of spheres per unit cell = 1/8 × 8 = 1

Volume of the sphere = 4/3 πr³

Volume of the cube = a³= (2r)³ = 8r³

∴ Fraction of the space occupied = 1/3πr³ / 8r³ = 0.524

∴ % occupied = 52.4 %

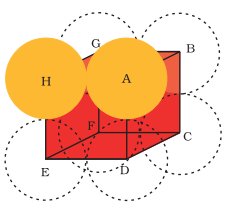
Body-centred Cubic Unit Cell

In body centred cubic unit cell

In $\Delta EFD$

Let DF= b

and we know that

ED=EF= a (edge length)

Now,

b² = a²+ a² = 2a²

In $\Delta AFD$

Let, AF = c

We know that

FD = b

& AD = a (edge length)

Now,

c² = a²+ b² = a²+ 2a²= 2a²

or c = √3 a

we know that c is body diagonal. As the sphere at the centre touches the sphere at the corner. Therefore body diagonal c = 4r

i.e. √3 a = 4r

or r = (√3/4)a

or a = 4r / √3

∴ Volume of the unit cell = a³ = (4r / √3)³ = 64r³ / 3√3

No. of spheres in bcc = 2

∴ volume of 2 spheres = 2 × 4/3πr³

Face-Centred Cubic (hcp and ccp Structures)

Let ‘r’ be the radius of sphere and ‘a’ be the edge length of the cube

As there are 4 sphere in fcc unit cell

∴ Volume of four spheres = 4 (4/3 πr³)

In fcc, the corner spheres are in touch with the face centred sphere. Therefore, face diagonal AD is equal to four times the radius of sphere

AC= 4r

But from the right angled triangle ACD

AC = √AD² + DC² = √a² + a²= √2a

4r = √2a

or a = 4/√2 r

∴ volume of cube = (2/√2 r)³

Watch this Video for more reference

Thus, it is concluded that ccp and hcp structures have maximum packing efficiency.

Solved Examples

Question 1:

An element crystallizes into a structure which may be described by a cubic type of unit cell having one atom in each corner of the cube and two atoms on one of its face diagonals. If the volume of this unit cell is 24 x 10^-24cm³ and density of the element is 7.20gm/cm³, calculate no. of atoms present in 200gm of the element.

Solution:

Number of atoms contributed in one unit cell = one atom from the eight corners + one atom from the two face diagonals = 1+1 = 2 atoms

Mass of one unit cell = volume × its density

= 24 × 10^–24 cm³ × 7.2 gm cm³

= 172.8 × 10^–24 gm

∴ 172.8 10^–24 gm is the mass of one – unit cell i.e., 2 atoms

∴ 200 gm is the mass = 2 × 200 / 172.8 × 10^–24 atoms = 2.3148 × 10²⁴ atoms

_________________________________________________________

Question. 2:

Calculate the void fraction for the structure formed by A and B atoms such that A form hexagonal closed packed structure and B occupies 2/3 of octahedral voids. Assuming that B atoms exactly fitting into octahedral voids in the HCP formed
by A

Solution:

Total volume of A atom = 6 × 4 / 3 πr_A³

Total volume of B atoms = 4 × 4/3 πr_A³ 4 × 4/3 π(0.414r_A)³

Since r_B/r_A as B is in octahedral void of A

Volume of HCP = 24√2r_A³

Packing fraction = 6 × 4/3 πr_A³ + 4 × 4/3 π (0.414r_A)³ / 24√2r_A³ = 0.7756

Void fraction = 1-0.7756 = 0.2244
____________________________________________________

Question 3:

Show by simple calculation that the percentage of space occupied by spheres in hexagonal cubic packing (hcp) is 74%

Solution:

Let the edge of hexagonal base =a

And the height of hexagon = h

And radius of sphere = r

The centre sphere of the first layer lies exactly over the void of 2^nd layer B.

The centre sphere and the spheres of 2^nd layer B are in touch

So, In Δ PQR (an equilateral triangle)

PR = 2r, Draw QS tangent at points

∴ In Δ QRS ∠QRS = 30°, SR = r

Cos30° = SR/QR

QR = r / √3/2 = 2r / √3

∴ PQ = √PR²– QR² = √4r² – 4r² / 3

h¹ = √8r² / 3 = 2 √2/3 r

∴ h = 2h¹ = 4 √2/3 r

Now, volume of hexagon = area of base x height

= 6 × √3 / 4 a² × h => 6 × √3/4 (2r)² × 4 √2/3 r

[∴ Area of hexagonal can be divided into six equilateral triangle with side 2r)

No. of sphere in hcp = 12 × 1/6 + 1/2 × 2 + 3 = 2+1+3 = 6

∴ Volume of spheres = 6 × 4/3πr³

∴ Percentage of space occupied by sphere = 6 × 4/3 πr³ / 6 × √3/4 × 4r² × 4√2/3 r × 100 = 74% ”

Calculation Involving Unit Cell Dimensions

From the unit cell dimensions, it is possible to calculate the volume of the unit cell. Knowing the density of the metal. We can calculate the mass of the atoms in the unit cell. The determination of the mass of a single atom gives an accurate determination of Avogadro constant.

Suppose edge of unit cell of a cubic crystal determined by X – Ray diffraction is a, d is density of the solid substance and M is the molar mass, then in case of cubic crystal

Volume of a unit cell = a³

Mass of the unit cell = no. of atoms in the unit cell × mass of each atom = Z × m

Here Z = no. of atoms present in one unit cell

m = mass of a single atom

Mass of an atom present in the unit cell = m/N_A

$Density\ of\ unit\ cell(d) = \frac{Mass\ of\ unit\ cell}{Volume\ of\ the\ unit\ cell}=\frac{z\times M}{a^3\times N_A}$

Density of the unit cell is same as the density of the substance.

Question 1: Packing efficiency of simple cubic unit cell is ..

a. 74.05%

b. 64.54%

c. 78.00%

d. 52.40%

Question 2: Which of the following crystal systems has minimum packing efficiency?

a. HCP

b. CCP

c. BCC

d. Simple Cubic

Question 3: Which of the following cubic unit cell has packing efficiency of 64%?

a. HCP

b. CCP

c. BCC

d. Simple Cubic

Question 4: For BCC unit cell edge length (a) =

a. 4r

b. 4r / √3

c. 4/√2 r

d. 2r

Question 5: For FCC unit cell, volume of cube =

a. 64 / 2√2 r³

b. 64r³ / 3√3

c. 25r³ / 3√3

d. 64/ 3r³

Q.1	Q.2	Q.3	Q.4	Q.5
d	d	c	b	a

Related Resources

You can also refer to Syllabus of chemistry for IIT JEE
Click here to get the Past year Papers of IIT JEE
Look here for Crystal Lattices and Unit Cells

To read more, Buy study materials of Solid State comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Chemistry here.

Live courses Ask question