Colligative Properties and Determination of Molar Mass
Table of contents |
Colligative Properties and Determination of Molar Mass
When we a non-volatile solute in a volatile solvent we observe that there is a decrease in vapour pressure of the solution. This decrease of vapour pressure can be quantitatively used to measure several properties of liquid solutions.These properties depend more on solute particles of the solution and are called colligative properties. The word “colligative” is derived from the Latin word “coligare” which means “to bind together”. The following properties come in the category of colligative properties.
-
Relative Lowering of Vapour Pressure
-
Elevation of Boiling Point
-
Depression of Freezing Point
-
Osmosis and Osmotic Pressure
Relative Lowering of Vapour Pressure
Image 1: There is a relative lowering of vapour pressure because less surface area is available for the solvent molecules to escape out.
The vapour pressure of a solvent is lowered when we add a non-volatile solute in it; this is called Lowering of Vapour Pressure. The French chemist François-Marie Raoult’s observed that the concentration of solute particles is mainly responsible for the lowering of vapour pressure and also discovered a relation between vapour pressure of solution, vapour pressure of pure solvent and mole fraction of solute and solvent.
Image 2: The vapour pressure decreases as we add solute in pure solvent
If the vapour pressure of the solution is P1, the vapour pressure of the pure solvent is P10 and mole fraction of solvent is x1, then according to Raoult’s Law:
P1 = P10 x1
The decrement in vapour pressure of solvent that is, Δ P1 will be
Decrement in Vapour Pressure = Vapour Pressure of Pure Solvent – Vapour Pressure of Solvent
Δ P1 = P10 – P1
Substituting P1 = P10 x1 in the above relation we get,
Δ P1 = P10 – P10 x1
Δ P1 = P10 (1 – x1)
Since the sum of mole fraction of solute ( x2) and mole fraction of solvent ( x1) is 1, we can write
1 – x1 = x2
Δ P1 = P10 x2
It is obvious that decrease in vapour pressure depends on mole fraction of solute (x2) as mentioned by Raoult’s.
The equation can be re-written as:
The term
is called Relative Lowering in vapour pressure and equals to mole-fraction of the solute.
If n1 and n2 are the respective moles of solute and solvent, then we can re-write the equation as:
If the solution is quite diluted, we can neglect moles of solute n1 in front of moles of solvent n2. So, in case of dilute solution, the equation becomes
We know that moles of any substance can be calculated by dividing the given mass by its molecular mass. Then moles of solute (n2) is equal to
where m2 and M2 are given mass and molecular mass of solute.
Similarly, a mole of solvent (n1) equals
Substituting the value of n1 and n2 in the dilute solution vapour pressure relation, we get
So, we know the other quantities, we can easily determine the molar mass of solute M2 with the above relation.
Example: The vapour pressure of pure benzene is 0.850 bars at room temperature. On addition of 0.6 g of non-volute solute in 39 g of benzene solution, the vapour pressure of benzene reduces to 0.845 bars. What is the molar mass of solute?
We have
P10 = 0.850 bar, P1 = 0.845 bar, m1 = 39 g, M1 = 78 g and m2 = 0.6 g. Now the unknown quantity is M2 which is the molar mass of non-volatile solute.
Using the relative lowering of vapour pressure relation, we get:
The change in vapour pressure Δ P1 = P10 – P1, equals to 0.850 – 0.845 = 0.05 bar. Substituting the respective values in the relation we get
Calculating, we get the value of M2 as 20.68 g.
Image 2: There is a relative lowering of vapour pressure because less surface area is available for the solvent molecules to escape out.
Elevation of Boiling Point
We know that on addition of non-volatile solute in a solvent, the vapour pressure of the solvent decreases. However the boiling point of the solution is greater than that of the pure solvent, this is because vapour pressure is directly proportional to temperature. And in order to boil a solution, we need to raise the boiling point of the solution to a certain temperature. This raising of temperature is called elevation of boiling point and just like the relative lowering of vapour pressure it also depends on solute particles in the solution.
Mathematically, if Tb0 is the boiling point of pure solvent and Tb denotes boiling point of the solution, then elevation in boiling point (denoted by Δ Tb) is
Δ Tb = Tb – Tb0
Experimentally it has been found that elevation in boiling point in dilute solutions is directly proportional to molality ‘m’ of solute present in a solution.
Δ Tb ∝ m
Δ Tb = Kb m
The term molality ‘m’ denotes the number of moles of solute present in 1000 g or 1 kg of solvent. In the relation Kb is the called molal elevation constant or ebullioscopic constant. The standard unit of molal elevation constant Kb is K kg mol-1.
Let m1 and m2 be the given masses of solvent and solute respectively. And molar masses of solute be M2 and that of solvent is M1, then molality can be evaluated from the relation:
Putting the value of molality in the boiling elevation relation, we get
Hence, if know the remaining quantities we can easily determine the molar mass of solute with the boiling elevation relation.
Example: The boiling point of a pure liquid is 353.23 K. If we add 2.70 g of a non-volatile solute in 90 g of liquid, the boiling point of the solution rises to 354.11 K. What will be the molar mass of non-volatile solute? Take the value of Kb of liquid to be 2.53 K kg mol-1.
So we have
Tb0 = 353.23 K, Tb = 354.11 K, m2 = 2.70 g, Kb = 2.53 K kg mol-1 and m1 = 90 g.
The elevation in boiling point Δ Tb = Tb – Tb0 = 354.11K – 353.23K =0.88
Using the above relation we get:
Calculating by we get the value of M2 to be 86.25 g, hence molar of the mass of solute is 86.25 g.
Depression of Freezing Point
When the vapour pressure of a solution is reduced, the freezing of the solution decreases. The freezing point of a solution is defined as the temperature at which vapour pressure of its substance become equal in liquid and vapour phase. If the vapour pressure of the solution equals to vapour pressure of the pure solvent, then the solution will be frozen. According to Raoult’s Law when we add a non-volatile solute in a solvent we find that the freezing point of the solution is slightly less than that of the pure solvent. This is called depression of freezing point.
The freezing point depression is denoted by Δ Tf and equals to
Δ Tf = Tf0 - Tf
The freezing point depression for dilute solutions is directly proportional to molality of the solute, just like the boiling elevation point. That is
Δ Tf ∝ m
Δ Tf = Kf m
The proportionality constant Kf is called Molal Depression Constant and is also known as Cryoscopic Constant, which depends upon the nature of the solvent.
We know that molality ‘m’ equals to
where m2 is a mass of solute, m1 is a mass of solvent and M2 is the molar mass of added non-volatile solute.
Putting the value of molality in above equation we get depression in freezing point as
Hence, we can use depression of freezing point to evaluate molar mass of solute.
Image 3: A brain map to remember how to calculate the molar mass of solute when depression in freezing point is given.
The table below depicts boiling and freezing points of important solvents with their molal constants.
|
Solvent |
Boiling Point (K) |
Kb ( K kg mol-1) |
Freezing Point (K) |
Kf ( K kg ol-1) |
|
Water |
373.15 |
0.52 |
273 |
1.86 |
|
Ethanol |
1.20 |
155.7 |
1.99 |
|
|
Cyclohexane |
353.74 |
2.79 |
279.55 |
20 |
|
Benzene |
353.3 |
2.53 |
278.6 |
5.12 |
|
Chloroform |
334.4 |
3.63 |
209.6 |
4.79 |
|
Acetic Acid |
391.1 |
2.93 |
290 |
3.90 |
|
Diethyl Ether |
307.8 |
2.02 |
156.9 |
1.79 |
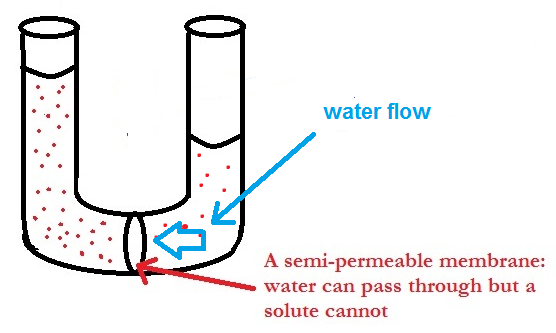
Osmosis and Osmotic Pressure
Image 4: Osmosis process
Osmosis is defined as the flow of liquid through a semi-permeable membrane which allows only solvent molecules to pass through it. The term membrane can be well-understood from real life examples like blood cells get destroyed when placed in a salt-water solution, raw mangoes get shrined when we prepare pickles with brine solution etc. A membrane is a continuous sheet or film with a pore network embedded in such way that it allows only desired substances to flow through it. It can be natural like a pig’s bladder or it can be man-made as cellophane is.
The membrane which allows only small solvent molecules to pass through it and resist the flow of bigger solute molecules is called Semipermeable Membrane or SPM.
Osmotic Pressure is the defined as the extra pressure one can add to stop the solvent molecules to flow. In other words, the pressure exerted on a solution to prevent osmosis with the help of semi-permeable membrane is called Osmotic Pressure. Osmotic pressure is a colligative property and depends on solute particles of the solution. Experimentally for dilute solutions, osmotic pressure is
π = CRT
where π is osmotic pressure, R is gas constant, T is constant and C denotes concentration or molarity of the solution.
Molarity (C) is defined as moles of solute divided by the volume of solution in liters. Mathematically
C = n2 / V
where n2 is moles of solute and V is the volume of the solution. Putting the value of c in osmotic pressure we get
π = (n2 / V) R T
Since moles n2 = m2 /M2, where m2 is given mass and M2 is molar mass, we can derive a new relation between osmotic pressure and molar mass of solute M2 as
Thus, if we know the remaining quantities we can easily determine the molecular masses of solute. In fact, this method is used to determine molecular masses of several biomolecules, proteins, and polymers. The advantage of using osmotic pressure is that we use molarity of the solution instead of molality at standard room temperature.
We can also determine density of the solution with the relation
π = d g h
where π is osmotic pressure, d is density of the solution, g is acceleration due to gravity and h is height of the liquid column.
Image 5: Relation between osmotic pressure and density of the solution
Notes:
-
Two solutions which have same osmotic pressure are said to be isotonic solutions and when we separate these solutions by an SPM, osmosis never occurs
-
The solution with higher osmotic pressure as compared to other solution is called Hypertonic Solution
-
The solution with lower osmotic pressure as compared to other solution is called Hypotonic Solution
Applications of Osmosis
Osmosis process is of great utility in commercial and daily life. It has following applications:
-
Reverse Osmosis, (a process in which we reverse the direction of osmosis by applying larger pressure than osmotic pressure on the other side, which help in getting pure solvent out of the solution) is used to obtain fresh water from the sea water
Image 6: We add cellulose acetate to act as semipermeable membrane
-
Also, we use cellulose acetate membrane to obtain fresh water as it only allows pure water solvent molecules and is impermeable to impurities and ions present in contaminated water
Watch this Video for more reference
More Readings