Solved Examples
Question 1:
Arginine vasopressin is a pituitary hormone. It helps to regulate the amount of water in the body by reducing the flow of urine form kidneys. An aqueous solution containing 21.6 mg of vasopressin in 100 mL of solution had an osmotic pressure of 3.70 mm Hg at 25oC. What is molecular weight of hormone? 
Solution:
We know πV = nRT
πV = wB/mB RT
mB = wB×RT/πV …(i)
where wB = mass of solute (21.6× 10−3 g)
R = 0.0821 L atm K−1 mol−1
T = 298 K
V = 100/1000 = 0.1 L : π = 3.70/760 atm
From (i), mB = 21.6×10–3×0.0821×298/(3.70/760)×0.1 = 1085 g/mol
________________________________________________________________
Question 2:
A solution is prepared by dissolving 1.08 g of human serum albumin, a protein from blood plasma, in 50 cm3 of aqueous solution. The solution has an osmotic pressure of 5.85 mm Hg at 298 K
(a) What is molar mass of albumin?
(b) What is height of water column placed in solution?
Given that density of water is 1gm cm3 .
Solution:
(a) Molar mass of albumin cab be calculated using followed relation
mB = wB×RT/πV …(i)
Given wB = 1.08; R = 0.0821 litre atm K−1 mol−1
T = 298 K, π = 5.85/760 atm; V = 50/1000 = 0.05 litre
Substituting these values in (i)
mB = 1.08×0.0821×298/(5.85/760)×0.05 = 68655 g/mol
(b) π h dg
5.85/760 × 1010325 = h × 1 × 10–3 × 9.8
∴ h = 7.958 × 10−2 m = 7.958 cm
_______________________________________________________
Question 3:
Calculate osmotic pressure of 5% solution of cane sugar (sucrose) at 15oC.
Solution:
m = mol. mass of sucrose (C12H22O11) = 342
w = 5 g,
V = 100 mL = 0.1 litre
S = 0.082,
T = (15 + 273) = 288 K
Applying the equation PV = w/m ST,
P = 5./342 × 1/0.1 × 0.082 × 288 = 3.453 atm
_________________________________________________________
Question 4:
The solution containing 10 g of an organic compound per litre showed an osmotic pressure of 1.16 atmosphere at 0oC. Calculate the molecular mass of the compound (S = 0.0821 litre atm per degree per mol.)
Solution:
Applying the equation
m = w/PV . ST
Given w = 10 g, P = 1.18 atm, V = 1 litre, S = 0.0821 and T = 273 K.
m = 10/1.18×1 × 0.0821 × 273 = 189.94
_____________________________________________________________
Question 5:
On dissolving 10.8 glucose (m.w. = 180) in 240 g of water, its boiling point increases by 0.13oC. Calculate the molecular elevation constant of water.
Solution:
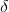 T = 100K'×w/W×m
T = 100K'×w/W×m
or K' = 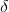 T×W×m/100×w
T×W×m/100×w
Given, 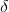 T =0.13oC, W = 240 g, m = 180 and 2 = 10.8 g
T =0.13oC, W = 240 g, m = 180 and 2 = 10.8 g
K' = 0.13×240×180/100×10.8 = 5.2 oC
_________________________________________
Question 6:
A solution of 2.5 g of a non-volatile solid in 100 g benzene boiled at 0.42oC higher than the boiling point of pure benzene. Calculate the molecular mass of the substance. Molal elevation constant of benzene is 2.67 K kg mol−1.
Solution:
m = 1000Kb×w/W×?T
Given, Kb = 2.67, w = 2.5 g, W = 100 g, T = 0.42
m = 1000×2.67×2.5/100×0.42 = 158.9
The molecular mass of substance is 158.9.
___________________________________________________
Question 7:
The molal elevation constant for water is 0.56 K kg mol−1. Calculate the boiling point of a solution made bt dissolving 6.0 g of urea (NH2CONH2) in 200 g of water.
Solution:
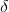 T = 1000Kb×w/m×W
T = 1000Kb×w/m×W
Given, Kb = 0.56 K kg mol−1, w = 6.0 g, W = 200 g, m=60
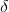 T = 1000×0.56×6.0/200×60 = 0.28oC
T = 1000×0.56×6.0/200×60 = 0.28oC
Thus, The boiling point of solution = b.pt. of water + 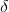 T = (100oC + 0.28oC) = 100.28oC
T = (100oC + 0.28oC) = 100.28oC
________________________________________________________________
Question 8:
By dissolving 13.6 g of a substance in 20 g of water, the freezing point decreased by 3.7oC. Calculate the molecular mass of the substance. [Molal depression constant for water = 1.863 K kg mol−1]
Solution:
m = 1000Kf× w/W×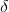 T
T
Given, Kf = 1.863 K kg mol−1.
w = 13.6 g, W = 20 g, 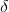 T = 3.7oC
T = 3.7oC
m = 1000×1.863×13.6/20×3.7 = 243.39
_______________________________________________________________
Question 9:
On dissolving 0.25 g of a non-volatile substance in 30 mL benzene (density 0.8 g/mL), its freezing point decreases by 0.40oC. Calculate the molecular mass of non-volatile substance (Kf = 5.12 K kg mol−1).
Solution:
Mass of benzene, W = volume × density = 30 × 0.8 = 24 g
Given, Kf = 5.12 K kg mol−1, w = 0.25 g, 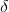 T = 0.40oC.
T = 0.40oC.
We know that
m = 1000Kf× w/W×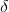 T
T
= 1000×5.12×0.25/24×0.40 = 133.33
________________________________________________________________
Question 10:
What is the volume of solution containing 1 g mole of sugar that will give rise to an osmotic pressure of 1 atmosphere at 0oC ?
Solution:
Applying the equation PV = nST,
V = n/P × S × T
Given n = 1, P = 1 atm, S = 0.821 and T = 273 K
V = 1/1 × 0.0821 × 273 = 22.4 litre
Related Resources
-
Click here to go through syllabus of chemistry for IIT JEE
-
Look here for reference books for chemistry
-
You can also refer methods of expressing concentration of solution
To read more, Buy study materials of Solutions comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Chemistry here.
View courses by askIITians


Design classes One-on-One in your own way with Top IITians/Medical Professionals
Click Here Know More

Complete Self Study Package designed by Industry Leading Experts
Click Here Know More

Live 1-1 coding classes to unleash the Creator in your Child
Click Here Know More

a Complete All-in-One Study package Fully Loaded inside a Tablet!
Click Here Know MoreAsk a Doubt
Get your questions answered by the expert for free
