Colligative Properties

A dilute solution is one in which the amount of the solute is very small in comparison to the amount of the solvent.The dilute solutions show more or less ideal behavior as the heat and volume changes, accompanying the mixing of solute and solvent, are negligible for all practical purposes. Dilute solutions obey Raoult’s law.

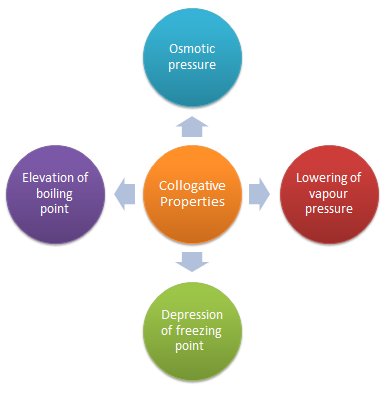
The properties of dilute solutions which depend only on number particles of solute present in the solution and not on their identity are called colligative properties (denoting depending upon collection).

We shall assume here that the solute is non volatile, so it does not contribute to the vapour. We shall also assume that the solute does not dissolve in solid solvent, that is, the pure solid solvent separates when the solution is frozen, the latter assumption is quite drastic, although it is true for many mixtures, it can be avoided.

Colligative properties are the properties of only dilute solution which are supposed to behave as ideal solutions. The various colligative properties are:

Depression of freezing point

Lowering of vapour pressure
Osmotic pressure
Elevation of boiling point

Lowering of Vapour Pressure by Non Volatile Solute

It has been known for a long time that when a non-volatile solute is dissolved in a liquid, the vapour pressure of the solution becomes lower than the vapour pressure of the pure solvent. In 1886, the French chemist, Francois Raoult, after a series of experiments on a number of solvents including water, benzene and ether, succeeded in establishing a relationship between the lowering of vapour pressure of a solution and the mole fraction of the non-volatile solute.

Let us consider a solution obtained by dissolving n moles of a non-volatile solute in N moles of a volatile solvent. Then mole fraction of the solvent, X₁ = N/(n+N) and mole fraction of the solute, X₂ = n /(N +n). Since the solute is non-volatile, it would have negligible vapour pressure. The vapour pressure of the solution is, therefore merely the vapour pressure of the solvent. According to Raoult's law, the vapour pressure of a solvent (P₁) in an ideal solution is given by the expression ;

P₁ = X₁ P₁⁰................(1)

where P₁⁰ is the vapour pressure of the pure solvent. Since X₁ + X₂ = 1, Eq. 1 may be written as

The expression on the left hand side of Equation (3) is usually called the relative lowering of vapour pressure. Equation (3) may thus be stated as: `The relative lowering of vapour pressure of a solution containing a non-volatile solute is equal to the mole fraction of the solute present in the solution.'

This is one of the statements of the Raoult's law.

Since mole fraction of the solute, X₂ is given by n/(N+n), Equation (3) may be expressed as

It is evident from Equation (4) that the lowering of vapour pressure of a solution depends upon the number of moles (and hence on the number of molecules) of the solute and not upon the nature of the solute dissolved in a given amount of the solvent. Hence, lowering of vapour pressure is a colligative property.

Refer to the following video for colligative properties

Determination of Molar Masses from Lowering of Vapour Pressure

It is possible to calculate molar masses of non-volatile non-electrolytic solutes by measuring vapour pressures of their dilute solutions.

Suppose, a given mass, w gram, of a solute of molar mass m, dissolved in
W gram of solvent of molar mass M, lowers the vapour pressure from P₁⁰ to P₁.
Then , by Equation (4)

Since in dilute solutions, n is very small as compared to N, Equation (5) may be put in the approximate form as

Limitations of Raoult’s Law

Raoult’s law is applicable only to very dilute solutions.
It is applicable to solutions containing non-volatile solute only.
It is not applicable to solutes which dissociate or associate in a particular solution.

Example 1 :

Question

The density of a 0.438 M solution of potassium chromate at 298 K is 1.063 g cm^-3. Calculate the vapour pressure of water above this solution. Given : P⁰ (water) = 23.79 mm Hg.

Solution

A solution of 0.438 M means 0.438 mol of K₂CrO4 is present in 1L of the solution. Now,

Mass of K₂CrO₄ dissolved per litre of the solution = 0.438 $\times$ 194 = 84.972 g

Mass of 1L of solution = 1000 $\times$ 1.063 = 1063 g

Amount of water in 1L of solution = 978.028/18 = 54.255 mol

Assuming K2CrO4 to be completely dissociated in the solution, we will have;
Amount of total solute species in the solution = 3 $\times$ 0.438 = 1.314 mol.

Mole fraction of water solution = 54.335/(54.335+1.314) = 0.976

Finally, Vapour pressure of water above solution = 0.976 $\times$ 23.79 = 23.22 mm Hg

Boiling Point Elevation by a Non-Volatile Solute

The boiling point of a liquid is the temperature at which its vapour pressure becomes equal to 760 mm (i.e. 1 atmospheric pressure). Since the addition of a non-volatile solute lowers the vapour pressure of the solvent, the vapour pressure of a solution is always lower than that of the pure solvent, and hence it must be heated to a higher temperature to make its vapour pressure equal to atmospheric pressure. Thus the solution boils at a higher temperature than the pure solvent. If T_b⁰ is the boiling point of the solvent and T_b is the boiling point of the solution, the difference in boiling points ( $\Delta$ T_b) is called the elevation of boiling point.

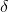Thus, T_b –T_b⁰ = $\Delta$ T_b.

$\Delta$ T_b a molality where $\Delta$ T_b = elevation of boiling point

n= no. of moles of non-volatile solute

N= Total no. of moles in the solution

This implies that the boiling point elevation in a dilute solution is directly proportional to the number of moles of the solute dissolved in a given amount of the solvent and is quite independent of the nature of the solute. Hence, boiling point elevation is a colligative property

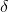$\Delta$ T_b = K_b $\times$ m

k_b : molal elevation constant or Ebullioscopic constant

m : molality of the solution

Molal boiling point elevation constant or ebullioscopic constant of the solvent, is defined as the elevation in boiling point which may theoretically be produced by dissolving one mole of any solute in 1000 g of the solvent.

where m₁ = molecular weight of solute and w and W are weights of solute and solvent.

Depression of Freezing Point by a Non-Volatile Solute

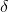Freezing point is the temperature at which solid and liquid states of a substance have the same vapour pressure. It is observed that the freezing point of the solution (T_f) containing non volatile solute is always less than the freezing point of the pure solvent (T_f⁰). Thus, T_f⁰ - T_f = $\Delta$ T_f

It can be seen that

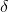$\Delta$ T_f $\alpha$ molality

that, is freezing point depression of a dilute solution is directly proportional to the number of moles of the solute dissolved in a given amount of the solvent and is independent of the nature of solute

or 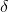$\Delta$ T_f = K_fm

k_f : molal freezing point depression constant of the solvent or cryoscopic constant

m : molality of the solution

Molal freezing point depression constant of the solvent or cryoscopic constant, is defined as the depression in freezing point which may theoretically be produced by dissolving 1 mole of any solute in 1000g of the solvent.

where m₁ = molecular weight of solute and w and W are weights of solute and solvent.

Osmosis and Osmotic Pressure

The phenomenon of the passage of pure solvent from a region of lower concentration (of the solution) to a region of its higher concentration through a semi-permeable membrane is called osmosis.

The driving force of osmosis is what is known as osmotic pressure. It is the difference in the pressure between the solution and the solvent system or it is the excess pressure which must be applied to a solution in order to prevent flow of solvent into the solution through the semi-permeable membrane. Once osmosis is complete the pressure exerted by the solution and the solvent on the semi-permeable membrane is same.

Van't Hoff equation for dilute solutions is ( parallel to ideal gas equation)

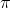$\pi$ V = nRT

where 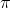$\pi$ = Osmotic pressure

V= volume of solution

n= no. of moles of solute that is dissolved

R = Gas constant

T= Absolute temperature

Isotonic Solutions : A pair of solutions having same osomotic pressure is called isotonic solutions.

Reverse Osmosis

When a solution is separated from pure water by a semipermeable membrane, water moves towards solution on account of osmosis. This process continues till osmotic pressure becomes equal to hydrostatic pressure or osmosis can be stopped by applying external pressure equal to osmotic pressure on solution. If external pressure greater than osmotic pressure is applied, the flow of solvent molecules can be made to proceed from solution towards pure solvent, i.e., in reverse direction of the ordinary osmosis. This type of osmosis is termed reverse osmosis. Reverse osmosis is used for the desalination of sea water for getting fresh drinking water.

Determination of osmotic pressure: Berkeley and Hartley’s method

Various methods are employed for the measurement of osmotic pressure but the best known method was suggested by Berkeley and Hartley. The apparatus used is shown in Fig. 5.11. A porcelain tube having copper ferrocyanide membrane in its walls in enclosed in a metallic jacket. The porcelain tube is fitted with a reservoir of pure solvent at one end and a capillary tube at the other end. In a metallic jacket is an arrangement for applying external pressure which is measured with the help of pressure eggs.

Procedure:

The porcelain tube is filled with pure solvent and the metallic jacket with solution. The level in the capillary tube will tend to move down as the solvent flows towards solution due to osmosis. External pressure is now applied on the solution by the piston so that level in capillary remain stationary. The reading of pressure gauge is recorded. This is the osmotic pressure of the solution.

Berkeley and Hartley’s method

Advantages:

It is a quick and accurate method.
The concentration of the solution does not change because flow of solvent is not permitted into solution; so the results obtained by this method are reliable.
As the osmotic pressure is balanced by external pressure, there is no strain on membrane and the danger of its bursting is eliminated. So, this method can be used to measure high osmotic pressure also.

Comparison of osmotic pressures:

de-Vries developed an approximate method for comparing the relative osmotic pressures of aqueous solutions. A solution of low osmotic pressure is termed hypotonic and solution of high osmotic pressure is termed hypotonic. The protoplasmic layer, lining the cell walls of plant cells is easily penetrated by water but us almost impermeable to the substances dissolved in the cellular fluid.
When a plant cell is placed in hypotonic solution, the water is drawn in and the cell swells. If the cell is placed in a hypertonic solution, water will diffuse out of the cell fluid and partial collapse of the cell will take place when potonic solution is separated from hypertonic solution using semipermeable membrane then osmosis takes place from hypotonic to hypertonic because solvent concentration is greater in hypotonic solution. this phenomenon is known as plasmolysis.
The change in cell can be placed in the solution of same osmotic pressure as that of the cell fluid, no change in the structure of the cell is observed. Such solutions having some osmotic pressures are termed isotonic. By putting, therefore, cells of the same kind into solutions of different concentrations, it can be ascertained whether the solution is hypertonic or hypotonic or isotonic.

Hypertonic, Hypotonic. Isotonic

Relation between osmotic pressure and vapour pressure

Let an aqueous dilute solution filled in a capillary tube is closed at one end by semipermeable membrane. The tube is placed in pure solvent (water). Entire apparatus is closed by a belljar. At osmotic equilibrium, the belljar is saturated with water vapour. At equilibrium osmotic pressure (π) becomes equal to hydrostatic pressure.

1214_Relation between osmotic pressure and vapour pressure.JPG

π = h × d …(i)

where ‘h’ is height in the column, π is osmotic pressure

Let p₀ = Vapour pressure of pure solvent

p = Vapour pressure of solution

Pressure at level L₁ = p₀; Pressure at level L₂ = p. Pressure at L₁ will be greater than pressure at L₂. Then

P₀ – p = hD …(ii)

where ‘d’ is density of solvent vapour of pressure p₀.

Dividing Eq. (i) by (ii), we have,

$\frac{\pi }{p_o -p}=\frac{h\times d}{h\times D}=\frac{h}{D}$

at a fixed temperature d/D is constant.

∴ π = constant (p₀ − p) …(iii)

i.e., π ∝ (p₀ – p) or $\Delta$ p …(iv)

Thus, osmotic pressure is directly proportional to the lowering of vapour pressure.

We know that p₀V = nRT

$p_oV =\frac{W}{M}RT$

i.e.

$p_oV =\frac{W}{V}RT = DRT$

$\therefore p_o=\frac{RTD}{M}$ ….............(v)

Dividing Eq. (iii) by (v), we get

$\frac{p_o-p}{p_o}=\pi \frac{M}{dRT}$

$\frac{\Delta p}{p_o}=\pi \frac{M}{dRT}$

At a fixed temperature, π and M/dRT are constant.

Thus, $\Delta$ p/p₀ ∝ π, i.e., Osmotic pressure is proportional to relative lowering of vapour pressure.

Question 1: Colligative properties depend only on

a. volume

b. pressure

c. temperature

d. number of particles

Question 2: Which of the following alternatives does not represent a colligative property?

a. Lowering of vapour pressure

b. Osmosis

c. Elevation of boiling point

d. Depression of freezing point

Question 3: The driving force of osmosis is

a. osmotic pressure

b. vapour pressure

c. surface tension

d. viscosity

Question 4: Such solutions having some osmotic pressures are termed

a. isobaric

b. isochoric

c. isotopic

d. isotonic

Q.1	Q.2	Q.3	Q.4
d	b	a	d

Related Resources

You can also refer to the syllabus of IIT JEE
Click here for reference books of chemistry
Look here for methods of expressing concentration of solution

To read more, Buy study materials of Solutions comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Chemistry here.

Live courses Ask question