Raoult’s Law
-
Vapour Pressure
 Consider a pure liquid in a beaker is covered with a jar. Some molecules on the liquid surface evaporate and fill the vacant space available to them. The molecules in the vapour phase move randomly in the vacant space, during this motion, they strike the surface of the liquid and condensed. This process of evaporation and condensation go on and an equilibrium is established between evaporation and condensation. The pressure exerted by vapours over the liquid surface at equilibrium is called vapour pressure of the liquid.
Consider a pure liquid in a beaker is covered with a jar. Some molecules on the liquid surface evaporate and fill the vacant space available to them. The molecules in the vapour phase move randomly in the vacant space, during this motion, they strike the surface of the liquid and condensed. This process of evaporation and condensation go on and an equilibrium is established between evaporation and condensation. The pressure exerted by vapours over the liquid surface at equilibrium is called vapour pressure of the liquid.
If solute is non volatile solid or liquid the vapour pressure of solution is equal to partial vapour pressure of solvent in the solution and if the solute is volatile solid or liquid, then vapour pressure will be equal to the sum of partial vapour pressure of solute and that of solvent.


-
Statement of The Roults Law
“The partial vapour pressure of any component in the solution is directly proportional to its mole fraction”. PA = KXA
XA = Mole fraction of A in solution
For pure liquids XA = 1
Then K = P0A Where P0A is the vapour pressure of component A in pure state
Hence, PA = XAP0A
Similarly for component B , PB = XBP0A
Roults law is applied for a solution of liquid in liquids
Refer to the following video for Raoult’s Law
Raoult’s Law in Combination with Dalton’s Law of Partial Pressure
Assuming that vapours of a liquid is behaving like an ideal gas, then according to Dalton’s law of partial pressure, the total pressure PT is given by
PT = PA + PB
or PT = XAP0A + XBP0B = XAP0A +(1- XA)P0B
Composition of the Vapour:
The composition of the liquid and vapour that are in mutual equilibrium are not necessarily the same, the common sense suggest that the vapour pressure should be richer in the more volatile component. This expectation can be confirmed as follows:
Let the mole fractions of A and B in vapour phase be YA and YB, then from Dalton’s law,

Condensation of vapours of solution:
When the vapours of solution (containing liquids A and B) is condensed, the composition of liquids A and B in the condensate remains same. The vapours over condensate can again recondensed and the composition of A and B in condensate (2) remains same as it was in vapour phase over condensate (2).

Raoult’s Law as a special case of Henry’sLaw
According to Raoult’s law, pi = xi pi0. ...(i)
In the solution of a gas in a liquid, one of the components is so volatile that it exists as a gas and we have already seen that its solubility is given by
According to Henry’s law p = KH x ….......(ii)
If we compare the equations for Raoult’s law and Henry’s law, it can be seen that the partial pressure of the volatile component or gas is directly proportional to its mole fraction in solution. Only the
proportionality constant KH differs from p10.
Thus, Raoult’s law becomes a special case of Henry’s law in which KH becomes equal to p10
Example 1: |
Question:The vapour pressure of two pressure liquids A and B that forms an ideal solution at 300 and 800 torr respectively at temperature T. A mixture of the vapours of A and B for which the mole fraction A is 0.25 is slowly compressed at temperature T. Calculate:
Solution:(a) pB0 = 300 torr pB0 = 800 torr yA = pA/P = pA0xA/P where yA and yB are mole fraction of A and B in the vapour yB = pB0xA/P ∴ yA = yB = pB0xA/pB0xB 0.025/0.75 = 300xA/800xB i.e., xA/xB = 8/9 i.e., xA = 8/17 = 0.47 Composition of last drop: xB = 9/17 = 0.53 (B) Pressure of last drop: p = pA0xA + pB0xB (c) At boiling point: p = 760 760o = 300 xA + 800 (1−xA) xA = 0.08, ∴ xB = 0.92 (d) For last drop: xA = 0.25, xB = 0.75 P = 300 × 0.25 + 800 × 0.75 = 675 torr. (e) yA = pA/P yA = 300×0.25/675 = 0.111 yB = 0.889 Here, yA and yB are composition of vapour of last drop. |
Partial pressure of immiscible liquids
Let ‘A’ and ‘B’ be the two volatile and immiscible liquids; pA and pB be the partial pressures of ‘A’ and ‘B’ respectively.
Then

where mA and mB are molar concentrations of ‘A’ and ‘B’ respectively.

Where WA, WB are weights of ‘A’ and ‘B’ and MA, MB are molecular weights of ‘A’ and ‘B’ respectively.
Ideal and Non – Ideal Solutions
The solutions which obey Raoult’s law at all compositions of solute in solvent at all temperature are called ideal solutions.
Ideal solutions can be obtained by mixing two components with identical molecular size, structure and they should have almost same inter molecular attraction e.g., two liquids A and B form an ideal solution when A –A and B–B molecular attractions will be same and hence A–B molecular atrraction will be almost same as A–A and B–B molecular attraction.
 An ideal solution should have following characteristics
An ideal solution should have following characteristics
-
It should obey Raoult’s law i.e., PA = XA and PB = XB
-
 Hmixing = 0, i.e. no heat should be absorbed or evolved during mixing
Hmixing = 0, i.e. no heat should be absorbed or evolved during mixing -
 Vmixing = 0, i.e. no expansion or contraction on mixing ?
Vmixing = 0, i.e. no expansion or contraction on mixing ?
Examples of Ideal solutions
-
Ethyl chloride and ethyl bromide
-
n–hexane and n–heptane
-
CCl4 and SiCl4
The solution which deviate from ideal behaviour are called non ideal solution or real solutions and they do not obey Raoult’s law over entire range of composition.
It has been found that on increasing dilution, a non ideal solution tend to be ideal.
For non ideal solutions,
-
PA
 XAP0A, PB ¹ XBP0B i.e, they do not obey Raoult’s law
XAP0A, PB ¹ XBP0B i.e, they do not obey Raoult’s law -
 Hmixing
Hmixing  0,
0, -
 Vmixing = 0
Vmixing = 0
Here we may have two cases
Case 1:

Such a solution show positive deviation from Raoult’s Law and the observed boiling point of such solutions is found to be less than the calculated value. e.g. cyclohexane and ethanol. In ethanol the molecules are held together due to hydrogen bonding, when cyclohexane is added to ethanol the molecules of cyclohexane tend to occupy the space between ethanol molecules due to which some hydrogen bonds break due to which inter molecular attraction between cyclohexane and ethanol is reduced and hence show higher vapour pressure.

Examples of solutions showing positiveedeviation:
-
Acetone + Ethanol
-
Acetone- Benzene
-
Water + Methanol
-
Water + Ethyanol
Case 2:

Solutions of above type show negative deviation from Raoult’s law and their observed boiling point is found to be higher than the calculated value eg. When acetone and chloroform are mixed together a hydrogen bond is formed between them which increases inter molecular attraction between them and hence decreases the vapour pressure

Examples of solutions showing negative deviation:
-
Acetone + Aniline
-
Chloroform + Diethyl ether
-
Chloroform + Benzene
-
Water + HCl
Condition for forming non-ideal solution showing positive deviation
Two liquids A & B on mixing form this type of solutions when
-
A-B attractive force should be weaker than A-A and B-B attractive force.
-
“A” and “B” have different shape, size and character.
-
“A” and “B” escape easily showing higher vapour pressure than the expected value.
Condition for forming non-ideal solution showing negative deviation
Two liquids A & B on mixing form this type of solutions when
-
A-B attractive force should be greater than A-A and B-B attractive force.
-
“A” and “B” have different shape, size and character.
-
Escaping tendency of both “A” and “B” is lower showing lower vapour pressure than expected ideally.

Example 2: |
Question:The vapour pressures of ethanol and methanol are 44.5 mm and 88.7 mm Hg respectively. An ideal solution is formed at the same temperature by mixing 60 g of ethanol with 40 g of methanol. Calculate the total vapour pressure for solution and the mole fraction of methanol in the vapour. Solution:Mol. mass of ethyl alcohol = C2H2OH = 46 No. of moles of ethyl alcohol = 60/46 = 1.304 Mol. mass of methyl alcohol = CH3OH = 32 No. of moles of methyl alcohol = 40/32 = 1.25 ‘XA’, mole fraction of ethyl alcohol = 1.304/1.304+1.25 = 0.5107 ‘XB’, mole fraction of methyl alcohol = 1.25/1.304+1.25 Partial pressure of ethyl alcohol = XA. pA0 = 0.5107 × 44.5 = 22.73 mm Hg Partial pressure of methyl alcohol = XB.pA0 =0.4893 × 88.7 = 43.73 m Hg Total vapour pressure of solution = 22.73 + 43.40 = 66.13 mm Hg Mole fraction of methyl alcohol in the vapour = Partial pressure of CH3OH/Total vapour pressure = 43.40/66.13 = 0.6563 |
Azeotropes
The non-ideal solutions showing large deviations from Roult’s law cannot be purified by distillation.
A solution at certain composition which continues to boil at constant temperature without change in the composition of the solution is called an Azeotrope or Constant boiling mixture.
Azeotropes with minimum vapour pressure and Minimum boiling point:
When liquid in a solution do not have great chemical affinity for each other their higher escape tendencies increase the vapour pressure much more than expected on the basis of Roult’s Law. In many cases the deviation are so extreme as to lead to a maximum in the curve. The point of maximum vapour pressure means that the boiling point at this composition will be minimum and constant.
Azeotropes with minimum vapour pressure and Maximum boiling point:
When liquids in solution show –ve deviation from ideality, their escape tendencies and hence the vapour pressure decreases than expected on the basis of Roult’s Law. In many cases, the maximum in the temperature composition curve is obtained. The point of minimum vapour pressure in the curve means that the boiling point of this composition will be maximum and constant.
Comparison Between Ideal and Non-ideal Solutions
Ideal solutions |
Non-ideal solutions |
|
Positive deviation from Raoult’s law |
Negative deviation from Raoult’s law |
|
|
Obey Raoult’s law at every range of concentration. |
Do not obey Raoult’s law. |
Do not obey Raoult’s law |
|
|
|
|
|
|
|
|
|
P = pA + pB = pA0XA + pB0XB |
pA > pA0XA; pB > pB0XB ∴ pA + pB > pA0XA + pB0XB |
pA < pA0XA; pB < pB0XB ∴ pA + pB < pA0XA + pB0XB |
|
A—A, A—B, B—B interactions should be same, i.e., ‘A’ and ‘B’ are identical in shape, size and character. |
A—B attractive force should be weaker than A—A and B—B attractive forces. ‘A’ and ‘B’ have different shape, size and character. |
A—B attractive force should be greater than A—A and B—B attractive forces. ‘A’ and ‘B’ have different shape, size and character. |
|
Escaping tendency of ‘A’ and ‘B’ should be same in pure liquids and in the solution. |
‘A’ and B’ escape easily showing higher vapour pressure than the expected value. |
Escaping tendency of both components ‘A’ and ‘B’ is lowered showing lower vapour pressure than expected ideally. |
Theory of Fractional Distillation


Consider the distillation of a mixture of composition x. The vapour given off has the composition x1. The composition of residual liquid will shift towards A. In the mean time the composition of the distillate shifts towards C. ultimately by repeated fractional distillation, the mixture of composition C will be obtained as distillate and pure liquid A will be left as residue. It will never be possible to have pure B.
When a mixture of composition y is distilled, the vapour given off has the composition y1, i.e., the composition of residual liquid will shift towards B. Ultimately the mixture of composition C will be obtained as distillate and pure liquid B will be left as residue. It will never be possible to have pure A.
There are several quid pairs which form minimum boiling point azeotropes. Some examples are given in the following table.
|
Mixture |
% Composition of azeotrope |
Boiling point (pressure = 1 atm) |
|
|
1. 2. 3. 4. |
Water-Ethanol Pyridine-Water Ethanol-Benzene Acetic acid-Toluene |
95.97 Ethanol 57.00 Pyridine 32.40 Ethanol 28.00 Acetic-acid |
78.13oC 92.6oC 67.8oC 105.4oC |

liquid and vapour phases have been shown in Fig. 5.4. The curves meet at point C. At this point both liquid and vapour phases have same composition. The constant-boiling mixture has maximum boiling point.
Consider distillation of a mixture of composition x. The vapour coming off is richer in A as indicated by composition x1. The composition of the residual liquid shifts towards C. As the distillation proceeds, the composition of the distillate moves towards A and that of residue towards. C.
Similarly, a mixture of composition lying between B and C, say y, on distillation will gie vapour richer in B as indicated by composition y1. The composition of residual liquid shifts towards C and distillate towards A on repeated distillation.
It is never possible to separate a mixture completely into the pure components A and B. It mainly gives a constant boiling mixture (azeotropes) which can never be separated by distillation.
There are several liquid pairs which form maximum boiling point azeotrope. Some examples are tabulated below:
|
|
Mixture |
% composition of azeotrope |
Boiling point (pressure = 1 atm) |
|
1. |
Nitric acid-Water |
68% Nitric acid |
125.5°C |
|
2. |
Acetic acid-Pyridine |
65% Pyridine |
139.0° C |
|
3. |
Chloroform-Aceton |
80% Chloroform |
65.0° C |
|
4. |
Hydrogen chloride-Water |
79.8% Water |
108.6° C |


Question 1: Enthalpy of mixing for an ideal solution is
a. 0
b. -ve
c. +ve
d. may be positive or negative depending on the nature of liquids
Question 2: For pure liquids XA =
a. 0
b. 1
c. 0.1
d. 0.5
Question 3: Which of the followings is not an ideal solution?
a. Ethyl chloride and ethyl bromide
b. n–hexane and n–heptane
c. CCl4 and SiCl4
d. Acetone and Aniline
Question 4: Which of the following solutions does not show positive deviation?
Acetone and Ethanol
Toluene and Benzene
Water and Methanol
Water and Ethyanol

|
Q.1 |
Q.2 |
Q.3 |
Q.4 |
|
a |
b |
d |
b |
Related Resources
-
Click here to go through syllabus of IIT JEE
-
Look here for reference books of chemistry
-
You can also refer methods of expressing concentration of solution
To read more, Buy study materials of Solutions comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Chemistry here.
View courses by askIITians


Design classes One-on-One in your own way with Top IITians/Medical Professionals
Click Here Know More

Complete Self Study Package designed by Industry Leading Experts
Click Here Know More

Live 1-1 coding classes to unleash the Creator in your Child
Click Here Know More

a Complete All-in-One Study package Fully Loaded inside a Tablet!
Click Here Know MoreAsk a Doubt
Get your questions answered by the expert for free

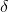 H
H