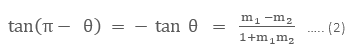Straight Line

 

Table of Content

What is Locus? How to find the equation to any locus? Define Straight line in simple words? What slope represents? Important points related to slope How to find the angle between two Straight Lines? What is the condition for the lines to be parallel? What is the Condition for the lines to be perpendicular? Equation of line parallel and perpendicular to a given line

 

What is Locus? How to find the equation to any locus?

Locus is the basis of the geometry. No any definition in geometry is complete without the introduction of the word ‘Locus’.

Locus is the set of points which follows or shares the common property. In other words, we can say that the locus is the path traced by any moving point or particle under specific conditions.

Example 1

Circle is the set of all those points which are equidistance from a fixed point (called the center of the circle) and this fixed distance is called as the Radius of the Circle.

In other words, the Circle is the locus of a point moving in such a condition that its distance from the fixed point is constant or always remains same.

Example 2

Let us take two fixed points A and B and a moving point P, moving in such a condition that its distance from the two fixed points, that is, A and B, is always fixed or do not change. So, in this condition, the path traced by the moving point will be a straight line and will be the perpendicular bisector of line joining A and B.

Below are the straight forward steps to find the equation to any locus of a point.

• Assume the coordinates of moving point P as (h, k) whose locus is to be determined.

• Using the given condition between the moving point and the fixed point, write a mathematical equation. This equation must involve the variables h and k.

• Eliminate the variable (s) (if any).

• At last, replace h by x and k by y to get the equation of required locus.

Example 3

Find the locus of point P if P is equidistant from points A(3, 4) and B(5, -2)

• Assuming P as (h, k).

• As per the given condition, we can write

• On Squaring the above equation and simplifying we get

4h – 12k = 4 or h – 3k = 1

Hence the locus of P is :-  x – 3y = 1

Note: - In the above problem, we don’t have any other variable and thus we haven’t followed the third step.
 

Define Straight line in simple words?

After learning locus, it’s easy to define straight line in terms of locus.

Straight line is the locus of a moving point P (h, k), which moves in such a condition that P is always collinear with the given two fixed points.

Also, we know from the concept of collinearity that, three points are collinear if they lie on a same straight line or the area of triangle from by these points is zero.

In Algebra, the linear equations (one, two or any number of variables) represents a straight line. That means, if one variable is changing (increasing or decreasing) linearly with the change in other variable, then the curve on graph will be a straight line. 

Example

 y = 5, 2x + 5y + 3 = 0, x = 2y – 5 are few examples of straight lines, but y = log(x), y = x², y = x + 1/x does not represent straight lines.

In this article, we will be discussing about straight lines in two variables only.

The general equation of straight line in two variables is represented as:

ax + by + c = 0

Where, a and b are the coefficients of x and y respectively and c is called as the Constant.

What slope represents?

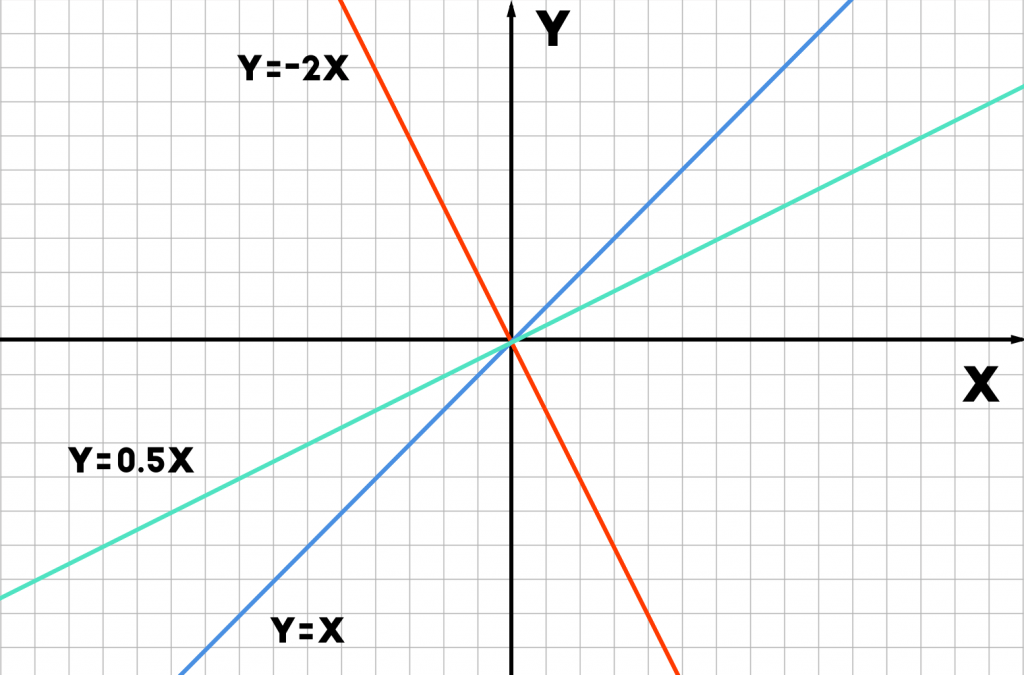
If we plot a straight line on a Cartesian (XY) plane, then we can see the inclination of the straight line with respect to the x – axis. This inclination or the angle between the straight line and the positive x – axis is termed as slope of a line.

In the Image above, we can observe different lines passing through same point (origin) but have different inclinations with the x – axis. This inclination is termed as the slope of the line.

Given a point, we can have infinite number of straight lines passing through it. This suggest us to have another condition for the same line to be uniquely represented on the XY plane. 

For example, A straight line passing through the origin and having the slope of 90^° or 270^° or – 90^° is the y – axis itself.

From the above example, we can learn two more points:

• For any specific line, if the slope is , then it will also have the slope of where n is any positive integer.

• The angle measured in anti-clock wise direction is taken as positive while the angle in clock wise direction is considered as negative.

If the inclination of any line from the positive x – axis is  then its slope is given by and is generally represented by m. Slope is also called as the Gradient.

Thus,

Note:-  can only lie in [0, 180^°) or [0 to -180^°).

Assume, two given points A (x₁, y₁) and B(x₂, y₂) given in the figure and a line passing through these points. As per the definition of slope, we can write

 

Important points related to slope

Since the slope is very important parameter in the straight line, we must take care of its all the important points.

• Since the slope =  (considering the to be positive i.e. angle is measured in the anti-clock wise direction) and thus the slope can positive or negative depending upon the quadrant of angle.

As we know from the basic trigonometry that the  is positive in first and the third quadrant. While it is negative in second and fourth quadrant. Thus, on the basis of this, we may say:

1. If 0 < θ < 90°

Slope will be positive as θ is positve

2. If 90° < θ < 180° 

Slope will be negative as  is positve

• If θ, which means the inclination towards x – axis is zero. This will represent a straight line parallel to x – axis.

Whereas, if θ = 90°, then the line will be perpendicular to x -axis or parallel to the y – axis.

• For the Points A(x₁, y₁) and B(x₂, y₂), the slope will calculated as:

How to find the angle between two Straight Lines?

If the equation of straight line is expressed in the form:

Y = mx + c

Then, the variable m is called as the Slope.

Let the equations of two straight lines be

L₁: Y₁ = m₁x + c₁  and L₂: Y₂ = m₂x + c₂

Let α and ß be the angles corresponding to slopes m₁ and m₂ respectively. Refer the diagram to understand the same.

That is, we have,

tan⁡ α = m₁

tan⁡ β = m₂

Then the angle between them will be θ and π – θ,  as represented in the figure.

Using the exterior angle property of the triangle, we can write

β = θ + α

Or,

θ = β - α 

Now we can apply tan both sides,

tan⁡ θ = tan ⁡(β- α)

Using tan (A – B) formula now,

On substituting the values of  and  from the above, we get

& the other angle will be 

Thus, from equation (1) and (2), we can say, The angle between two straight lines will be

What is the condition for the lines to be parallel?

If the two lines are parallel, then the angle between them will be zero.

Thus, In equation (3), replace

Since, tan 0 = 0

Therefore, m₁ = m₂

If L₁: a₁x + b₁y + c₁ = 0  and L₂: a₂x + b₂y + c₂ = 0 are parallel then

m₁ = m₂

What is the Condition for the lines to be perpendicular?

If the two lines are perpendicular, then the angle between them will be right angle or 90°.

Thus, In equation (3), replace

Since, tan 90^°= ∞ 

Therefore, 1 + m₁m₂ = 0 or m₁m₂ = -1

If L₁: a₁x + b₁y + c₁ = 0 and L₂: a₂x + b₂y + c₂ = 0 are parallel, then

m₁m₂ = -1

Equation of line parallel and perpendicular to a given line

If we are given a straight-line ax + by + c = 0,

Then, the equation of line parallel to the given line will be

ax + by + λ = 0

and the equation of line perpendicular to the given line will be

bx – ay + λ = 0.

Where, λ  is a constant whose value can be determined from the addition condition given in the problem.
 

More Readings

Straight Line

Related Resources:

• Click here to refer the most Useful Books of Mathematics.

• For getting an idea of the type of questions asked, refer the previous year papers.

To read more, Buy study materials of Straight Lines comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Mathematics here.