Angle between two Straight Lines

Table of Content

Angle Bisectors
Combined Equations of Angle Bisectors of Lines
Related Resources

Angle bisector of two lines (the line which bisects the angle between the two lines) is the locus of a point which is equidistant (having equal perpendicular distance) from the two lines.

Say, we have two lines

L1 : A1x + B1y + C1 = 0

L2 : A2x + B2y + C2 = 0

If point R(p, q) lies on the bisector, then length of perpendicular from P to be both lines should be equal.

i.e.

1877_Angle between two straight lines 2.JPG

generalizing for any point (x, y) the equation of the angle bisector is obtained as:

A1x+B1y+C1/√A12 + B12 = + A2x+B2y+C2/√A22 + B22

Note:

1. This equation gives two bisectors: one-acute angle bisector and the other obtuse bisector.

2. Rule to decide the particular bisector

To determine a bisector which lies in the same relative position with respect to the lines as a given point S(x3, y3) does, make the signs of the expressions A2x3 + B1y3+ C1 and A2x3 + B2y3 + C2 identical. (say positive) then A1x+B1y+C1/√A12 + B12 = +A2x+B2y+C2/√A22 + B22 gives the bisector towards this point. If the signs are different multiply one of the equations with ‘–1’ throughout, so that positive sign is obtained. Then above equation with changed equations of lines will given the required bisector.

3. If (x3, y3) ≡ (0, 0) and A2A1 + B2B1 > 0 then the bisector towards the origin is the obtuse angle bisector.

4. Alternative method: to determine whether the bisector is of the obtuse or acute angle, determines both the bisectors and calculate angle between one of them and the initial line. The bisector for which |tan θ| > 1 is the obtuse angle bisector.

IIT JEE, AIEEE study material is available online free of cost at askIITians.com. We offer numerous live online courses, online tests and other interesting sections as well for IIT JEE and AIEEE preparation – you do not need to travel anywhere any longer – just sit at your home and study for IIT JEE, AIEEE and other engineering exams live online with askIITians.com

Angle Bisectors

To find the equations of the bisectors of the angle between the lines

a1x + b1y+ c1 = 0 and a2x + b2y + c2 = 0.

A bisector is the locus of a point, which moves such that the perpendiculars drawn from it to the two given lines, are equal.

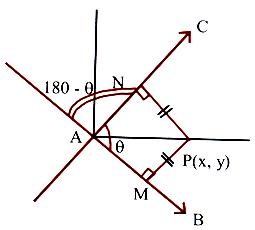
The equations of the bisectors are

a1x+b1y+c1/√a12+b12 = + a2x+b2y+c2/√a22+b22.

AP is the bisector of an acute angle if,

Tan (∠PAN) = tan (θ/2) is such that |tan θ/2| < 1.

AP is an obtuse angle bisector if,

Tan (∠PAN) = tan (θ/2) is such that |tan θ/2| > 1.

Notes :

When both c1 and c2 are of the same sign, evaluate a1a2 + b1b2. If negative, then acute angle bisector is a1x+b1y+c1/√a12+b12 = + a2x+b2y+c2/√a22+b22.
When both c1 and c2 are of the same sign, the equation of the bisector of the angle which contains the origin is a1x+b1y+c1/√a12+b12 = + a2x+b2y+c2/√a22+b22.
Bisectors of the angle containing the point (α, ß) is a1x+b1y+c1/√a12+b12 = +a2x+b2y+c2/√a22+b22 if a1α + b1ß + c1 and a2α + b2ß + c2 have the same sign.
Bisectors of the angle containing the point (α, ß) is a1x+b1y+c1/√a12+b12 = +a2x+b2y+c2/√a22+b22 if a1α + b1ß + c1 and a2α + b2ß + c2 have the opposite sign.

Illustration:

For the straight lines 4x + 3y – 6 = 0 and 5x + 12y + 9 = 0 , find the equation of the

(i) bisector of the obtuse angle between them,

(ii) Bisector of the acute angle between them,

(iii) bisector of the angle which contains (1, 2)

Solution:

Equations of bisectors of the angles between the given lines are

4x+3y–6/√42+32 = + 5x+12y+9/√52+122

⇒ 9x – 7y – 41 = 0 and 7x + 9y – 3 = 0.

If θ is the angle between the line 4x + 3y – 6 = 0 and the bisector 9x – 7y – 41 = 0, then tan θ = > 1.

Hence

(i) The bisector of the obtuse angle is 9x – 7y – 41 = 0.

(ii) The bisector of the acute angle is 7x + 9y – 3 = 0.

For the point (1, 2)

4x + 3y – 6 = 4 × 1 + 3 × 2 – 6 > 0.

5x + 12y + 9 = 12 × 12 + 9 > 0.

Hence equation of the bisector of the angle containing the point (1, 2) is 4x+3y–6/5 = 5x+12y+9/13 ⇒ 9x – 7y – 41 = 0.

Combined Equations of Angle Bisectors of Lines

Combined equations of the angle bisectors of the lines represented by ax2 + 2hxy +by2 = 0

Let ax2 + 2hxy + by2 = 9 represent lines

y – m1x = 0 and y – m2x = 0

Let P(α, ß) be any point on one of bisectors.

⇒ (ß–m1α)/√1+m12 = + ß–m2α/√1+m22

⇒ (1 + m22) (ß – m1α)2 – (1 + m12) (ß – m2α)2 = 0

⇒ Locus of P(α, ß) is

x2 – y2 = 2hxy 1–m1m2/m1+m1

⇒ x2–y2/a–b = xy/h; is required equation of angle bisectors …… (1)

Note:

1. If a = b, then bisectors are x2 – y2 = 0 i.e. x – y = 0, x + y = 0

2. If h = 0, the bisectors are xy = 0 i.e. x = 0, y = 0

3. If in (i), coefficient of x2 + coefficient of 2 = 0, then the two bisectors are always perpendicular to each other

Illustration:

Prove that the angle between one of the lines given by
ax2 + 2hxy + by2 = 0 and one of the lines given by ax2 + 2hxy+ by2 + K(x2 + y2) = 0 is equal to the angle between the other two lines of the system.

Solution:

Let L1 and L2 be one pair and L3 and L4 be the other pair of lines.

If the angle between L1 and L3 is equal to the angle between L2 and L4 then pair of bisectors of L1 and L2 would be same as that of L3 and L4. Pair of bisectors of L3 and L4 is

x2–y2/(a+k)–(b+k) = xy/h

⇒ x2–y2/a–b = xy/h

Which is the same as the bisector pair of L1 and L2.

6. Angle bisectors of ax2 + 2hxy + by2 + 2gx + 2fy + c = 0 (i) are given by (x–x0)2–(y–y0)2/a–b = (x–x0)(y–y0)/h where (x0, y0) is the point of intersection of (i)

Enquiry: If we shift the origin of the coordinate system how can the coordinates of a point be known in the new system? What will happen if we rotate the axis?

(i) Linear Transformation:

CP = x, DP = y; AP = x, BP = y

If origin is shifted to (h, k) then the coordinates of a point
P(x, y) in the new system are

X = x – h

Y = y – k

You can check it by putting (h = 0, k = 0) that it gets reduced to the same original coordinate system.

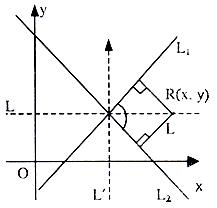
(ii) Rotation of Axes:

If axes are rotated anticlockwise by angle q then the coordinates of a point P(x, y) changes to say P(x, y):

OL = x, PL = y

OM = X, PM = Y

OP = R (say)

cos (α + θ) = x/R …… (i)

sin (α + θ) = Y/R …… (ii)

cos α = x/R …… (ii)

sin α = Y/R …… (iv)

Eliminating α from (i), (ii), (iii) and (iv) we get

X = x cos θ + y sin θ

Y = –x sin θ + y cos θ

It can be checked that if θ = 0; then coordinates remain unchanged.

Illustration:

Find the equation of the line 2x + y = 7 when co-ordinates system is shifted to the point (3, 1)

Solution:

x = 3 + X and y = 1 + Y

Equation of line becomes

2(3 + X) + (1 + Y) = 7

or 2X + Y = 0

Note:

Slope of the line remains the same.

The general equation of second degree ax2 + 2hxy + by2 + 2gx + 2fy + c=0 represents a pair of straight lines if 1994_Combined equations 1.JPG

= 0.

⇒ abc + 2fgh – af2 – bg2 – ch2 = 0 and h2 > ab.

The homogeneous second degree equation ax2 + 2hxy + by2 = 0 represents a pair of straight lines through the origin.

If lines through the origin whose joint equation is ax2 + 2hxy + by2 = 0, are y = m1x and y = m2x, then y2 – (m1 + m2)xy + m1m2x2 = 0 and y2 + 2h/b xy + a/b x2 = 0 are identical. If θ is the angle between the two lines, then tanθ = + √(m1+m2)2–4m1m2/1+m1m2 = + 2√h2–ab/a+b.

The lines are perpendicular if a + b = 0 and coincident if h2 = ab.

Related Resources

Click here to refer the most Useful Books of Mathematics.
For getting an idea of the type of questions asked, refer the previous year papers.

To read more, Buy study materials of Straight Lines comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Mathematics here.