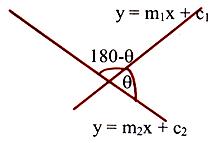Examples on Angle between two Straight Lines

Illustration:

Draw the lines 3x + 4y – 12 = 0 and 5x + 12y + 13 = 0. Find the equation of the bisector of the angle containing the origin. Also find the acute angle bisector and obtuse angle bisector.

Solution:

Let us make the expression on the left-hand side of the given equations of the same sign – or + ve. After substituting x = 0 and 
y = 0.

L.H.S. of (i) is 3.0 + 4.0 – 12 = – 12 = – ve

R.H.S. of (ii) is 5.0 + 12.0 + 13 = 13 = + ve

So, multiply equation (i) by (–1), we get

 – 3x – 4y + 12 = 0                                              …… (1)

Equation of the bisector of the angle containing origin is given by +ve sign i.e. –3x – 4y+12/5 = + 5x+12y+13/13

⇒ 64x + 112y – 91 = 0                                                …… (3)

Again, the given lines are

– 3x – 4y + 12 = 0                              …… (1)

5x –+ 12y + 13 = 0                             …… (2)

To find out whether this is an acute angle bisector or obtuse angle bisector, let us find the sign of a₁ a₂ + b₁ b₂ from equation (1) and equation (2).

a₁ a₂ + b₁ b₂

= (–3) (5) + (–4) (12) = – 15 – 48 = – 63 = – ve

the bisector containing the origin is the acute angle bisector.

Now, For obtuse angle bisector, we take –ve origin.

i.e. –3x – 4y+12/5 = + 5x+12y+13/13

i.e. 14x – 8y – 221 = 0                                                …… (4)

Well, to confirm all this, let us find angle between one of the lines and one of the bisectors i.e.

5x + 12y + 13 = 0                                              …… (2)

64x + 112y – 91 = 0                                           …… (3)

Slope of line (2) is m₂ = –5/12

Slope of line (3) is m₃ = –64/112

Let q be the angle between these two lines

⇒ tan θ =  < 1

∴  64x + 112y – 91 = 0 is an acute angle bisector.

If θ is the angle between two lines, then tanθ =    

(i) If the two lines are perpendicular to each other then m₁m₂ = –1.

Any line perpendicular to ax + by + c = 0 is of the form 
bx – ay + k = 0.

(ii) If the two lines are parallel or are coincident, then m₁ = m₂.

Any line parallel to ax + by + c=0 is of the form ax – ay + k=0.

Let there be two-lines l₁ and l₂ with slopes m₁ and m₂ respectively. So tan α = m₁, tan β = m₂ Angle between them is either

α – β or π – (α – β) depending on the side on considers

Now, tan (a – b) = tan α – tan β/1+tan α tan β

⇒ tan (θ) = m₁+m₂/1+m₁m₂                    (α – β = θ say)

Since lines can be taken in any order and

tan(– θ) = – tan θ. So only the magnitude of θ can be obtained.

Further tan (π – θ) = – tan θ.

Since magnitude also includes the other angle i.e.

Supplementary angle. So θ is given by

tan θ_acute = 

Important:

1. If lines are parallel

tan θ = 0 ⇒ m₁ = m₂

2. If lines are perpendicular

tan θ = tan (π/2) = ∝

1 + m₁ m₂ = 0 ⇒ m₁ m₂ = – 1

3. Equation of a line parallel to y = mx + c is y = mx + k, i.e. Equation of a line parallel to ax + by + c = 0 is ax + by + k = 0

4. Equation of a line perpendicular to y = mx + c is y = 1/m  x + k i.e. Equation of a line perpendicular to ax + by + c = 0 is 
bx – ay + k = 0

5. Lines          a₁x + b₁y + c₁ = 0                               …… (i)

                     a₂x + b₂y + c₂ = 0                               …… (ii)

        represents

(i) intersecting lines if a₁/a₂ ≠ b₁/b₂

(ii) parallel lines if a₁/a₂ = b₁/b₂

(iii) Coincident lines if a₁/a₂ = b₁/b₂ = c₁/c₂

To read more, Buy study materials of Straight Lines comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Mathematics here.