• Coordinate Geometry
• OFFERED PRICE: Rs. 1,484
• View Details

Pair of Straight Lines 



The equation ax2 + 2hxy + by2 + 2gx + 2fy + c = 0. Represents a second degree equation where a, h, b doesn’t variables simultaneously.

Let a ≠ 0.

Now, the above equation becomes

a2 x2 + 2ax (hy + g) = aby2 – 2afy – ac

on completing the square on the left side, we get,

a2 x2 + 2ax (hy + g) = y2 (h2 – ab) + 2y (gh – af) + g2 – ac.

i.e.    (ax + hy + g) = + √y2(h2–ab)+2y(gh–af)g2–ac

We cannot obtain x in terms of y, involving only terms of the first degree, unless the quantity under the radical sign be a perfect square. The condition for this is,

(gh – af)2 = (h2 – ab) (g2 – ac)

i.e. g2h2 – 2afgh + a2f2 = g2h2 – abg2 – abg2 – ach2 + a2bc

cancelling and diving by a, we have the required condition

abc + 2fgh – af2 – af2 – bg2 – ch2 = 0



Illustration:

What is the point of intersection of two straight lines given by general equation ax2+ 2hxy + by2 + 2gx + 2fy + c = 0?

Solution:

The general solution is

ax2 + 2hxy + by2 + 2gx + 2fy + c = 0                   …… (1)

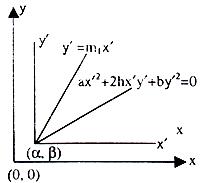
Let (α, ß) be the point of intersection we consider line paralleled transformation.

x = x’ + α,         y = y’ + ß

From (1) we have

a(x’ + α)2 + 2h(x’ + α) (y’ + ß) + b(y’ + ß)2 + 2g(x’ + α) + 2f(y’ + ß) + c = 0

⇒     ax’2 + 2hx’y’ + by’2 + a α2 + 2hαß + bß2 + 2gα + 2fß + 2x’(a α + hß + g) + 2y’ + 2y’ (hα + bß + f) = 0

⇒     ax’2 + 2hx’y’ + by’2 + 2x’(aα + hß + g) + 2g’ + 2y’ (hα + bß + f) = 0



Which must be in the form

ax'2 + 2hx’y’ + by’ = 0

This cannot be possible unless

aα + hß + g = 0

hα + bß + f = 0

Solving

α/hf–bg = ß/hg–af = 1/ab–h2

α = hf–bg/ab–b2, ß = hg–af/ab–h2



Illustration:

Represent lines y = 2x and y = 3x by a homogeneous equation of second degree

Solution:

(y – 2x) (y – 3x) = 0

Or 6x2 – 5xy + y2 = 0

 

Illustration:

Represent lines parallel to y = 2x and y = 3x by a second degree equation

Solution:

(y – 2x – c1) (y – 3x – c2) (where c1 and c2 are constants)

= 6x2 – 5xy + y2 + (3c1 + 2c2) x + (– c1 – c2) y + c1 c2 = 0

Note:

1. Homogeneous part is same as for the equation of above illustration. Therefore, the homogeneous part of a general second degree equation determines the slope of the lines i.e. lines parallel to ax2 + 2hxy + by2 + c = 0 and through the origin are represented by the equation ax2 + 2hxy + by2 = 0

2. The equation ax2 + 2hxy + by2 + 2fy + c = 0 represents a pair of parallel straight lines if h/a = b/h = f/g or bg2 = af2

The distance between them is given by 2√g2–ac/a(a+b) or √f2–bc/b(a+b)



Illustration:

Does the second degree equation x2 + 3xy + 2y2 – x – 4y – 6 = 0 represents a pair of lines. If yes, find their point of intersection.

Solution:

We observe that

a = 1, h = 3/2, b = 2, g = –1/2, f = 2, c = – 6

abc + 2fgh – af2 – bg2 – ch2 = – 12 + 3 – 4 – 1/2 + 27/2 = 0

Therefore the given second-degree equation represents a pair of lines, x2 + 3xy + 2y2 – x – 4y – 6 = (x + 2y + 2) (x + y – 3).

Consider the equations formed by first two rows of .

i.e. ax + hy + g = 0 and hx + by + f = 0

i.e. x + 3/2 y – 1/2 and 3/2 x + 2y – 2 = 0

Solving these, we get the required point of intersection.

i.e. 2x + 3y – 1 = 0

3x – 4y – 4 = 0

Solving the above equation, we get x = 8, y = –5.

Note:

(2x + 3y – 1)(3x + 4y – 4) ≠ x2 + 3xy + 2y2 – x – 4y – 6.

To read more, Buy study materials of Straight Lines comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Mathematics here.

• Complete JEE Main/Advanced Course and Test Series
• OFFERED PRICE: Rs. 15,900
• View Details Xpress Buy