Various forms of the Equation of a Line
Table of Content |
What is the formula to find the slope?
If the inclination of any line from the positive x – axis is θ then its slope is given by tan θ and is generally represented by m. Slope is also called as the Gradient.
Thus,
Note: - can only lie in [0 ,180°) or (-180, 0].
Assume, two given points A (x1, y1) and B(x2, y2) given in the figure and a line passing through these points. As per the definition of slope, we can write
Example
What will be the slope of a line passing through A(2, 6) and B(4 , -2)
(we can assume any point as (x1, y1) and other as (x2, y2))
What is the formula for the equation of a line?
Straight line is the locus of a moving point P (h, k), which moves in such a condition that P is always collinear with the given two fixed points. The inclination or the angle between the straight line and the positive x – axis is termed as slope of a line.
Now, we can also define straight line as the locus of moving point P (h , k) which moves in such a condition that the slope of this Point P with respect to the two fixed points are equal.
As per this definition, assume two fixed points as A (x1, y1) & B (x2, y2) and let the moving point be P (h, k).
Then we can say,
Or,
Above equation is the required equation or formula for a straight line using the given two fixed points.
Example
Find the equation of a straight line passing through A(2, -4) and B(0, 4)
Using the above formula, the equation will be,
On simplification we get,
4x + y – 4 = 0
The general equation of straight line in two variables is represented as:
ax + by + c = 0
Where, a and b are the coefficients of x and y respectively and c is called as the Constant.
What are the different forms for the equation of line?
Given a point, we can have infinite number of straight lines passing through it. This suggest us to have another condition for the same line to be uniquely represented on the XY plane.
For Example, A straight line passing through the origin and having the slope of 90° or 270° or – 90° is the y – axis itself.
So, depending upon the type of information available with us for a line, straight lines can be represented into different forms. These forms are as follows:
-
General form
-
Point - slope form
-
Two - point form
-
Slope – intercept form
-
Normal form or perpendicular form
Given the equation in any form, we can easily convert it into any other desired form.
We shall learn all these forms in the upcoming headings.
What is point – slope form of a line?
In Point – slope form of a line, we have the information about a point through which the line is passing and its slope.
Assume, a point A(x1 , y1) through which a line is passing and its slope be m.
For any moving point P, we can write,
Or,
y – y1 = m(x – x1)
The above form is the equation of straight line in point – slope form.
Example
Find the equation of a line having slope tan 120° and passes through (2,4).
As per given information, we have
A(x1, y1) = (2, 4) and m = tan 120° = tan(90°+ 30°) = – cot(30°) = – √3
On simplification we get,
How do you write an equation in standard form with 2 points?
Two point form of a straight line is already been derived in equation (1). So, we can directly say that the equation of a straight line passing through A(x1, y1) and B(x2, y2) can be represented as:
where, x and y are the coordinates of any general point P satisfying the above equation.
What is x and y intercept of a line?
If a line cuts the x – axis at any point, then the abscissa of that point is called as the x – Intercept of a line. Similarly, y – intercept is the ordinate of a point where the line cuts the y – axis. These intercepts can be positive or negative depending upon the point around origin where it cuts the axis.
If a line cuts x – axis at A and y – axis at B, then OA and OB will be the x – intercept and the y – intercept respectively. Where, O is the origin.
If a line does not cut any particular axis, then corresponding intercept will be infinity.
What is slope intercept form of a line?
If c is the y – intercept of a line, that means the line passes through a point (0, c). Now assuming the slope as m, we can write the equation as
y – c = m (x – 0)
on further simplification,
y = mx + c
This is the required equation in slope intercept form. Remember, here c is the y – intercept and not the x – intercept.
Find the equation of a line which cuts the y -axis at (0, -2) and has the slope of 5.
Since, the given line cuts the y – axis at (0, -2) and thus the y – intercept that is, c, will be – 2.
So, the equation of such line will be given by:
y = 5x – 2
Explain Intercept form of a line
Intercept form of a line is an equation of line which is obtained using x and y intercept.
If we have A (a, 0) and B (0 , b) as the x – intercept and y – intercept respectively, then the equation of a line in intercept form can be expressed as
Proof:
If A(a, 0) and B(0 , b) are the x – intercept and y – intercept respectively, then using the two point form of a line, we can write,
On simplification,
This is the required equation of a line in the intercept form.
Example
Find the equation of a line having x – intercept as - 3 and y – intercept as 4.
We have, a = -3 and b = 4, so
On further simplification, we get
4x – 3y + 12 = 0
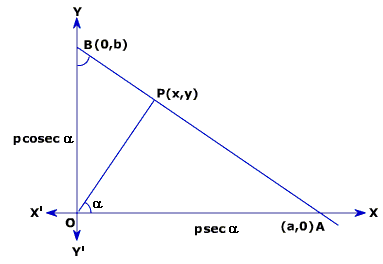
How to write any equation in normal form?
Consider a line AB, whose perpendicular distance from the center is p and let this perpendicular OP makes an angle of α with the x – axis.
In the figure, if angle OPA = 90° and angle POA is α, then angle OBP will also be equals to α.
Now, using basic trigonometry, in right triangle OPA,
Similarly, in right triangle BPO
Here, OA and OB are now x and y intercept for the line AB,
Thus, using the intercept form of a line,
Or,
x cosα + y sinα = p
This equation in the required equation in normal or perpendicular form.
Example
Find the equation of line whose perpendicular distance from the origin is 5 and this perpendicular makes an angle of 45° with the y – axis.
Since the perpendicular subtends an angle of 45° with y – axis and thus the same will be the angle with the x – axis.
Now, as per given information, we have,
p = 5 and α = 45°
So, the required equation of the line will be as:
x cos 45° + ysin 45° = 5
or,
x + y = 5√2
More Readings