Bohr Model

Table of Content

Angular Momentum
Energy of an Electron in ‘n’ th state En
Problem (JEE Advanced)
Related Resources

Sub Atomic Particle in an Atom

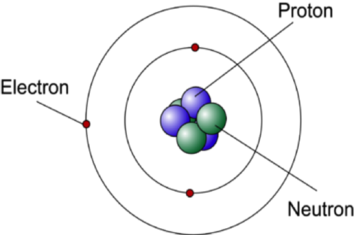
Bohr Model was introduced after the Rutherford’s model. It retained some of the features like the orbiting of nucleus and the electrons under the action of the Coulomb’s Law of electrostatic attraction. Various other concepts like radiation less orbits and stationary states were also introduced in the Bohr Model. We discuss the postulates of Bohr Atomic theory.

Bohr introduced the concept of radiation less orbits in which the electrons revolve as usual around the nucleus but without radiating any kind of energy which is contrary to the laws of electromagnetism. This was a hypothesis, but at least a working one.
Radiation occurred only when an electron made a transition from one stationary state to another. The difference between the energies of the two states was radiated as a single photon. Absorption occurred when a transition occurred from a lower stationary state to a higher stationary state.
He also introduced the correspondence principle which states that the spectrum is continuous and the frequency of light emitted equals the frequency of the electron.

Electrons Revolves Around the Orbit in an Atom

Neil Bohr explained the line spectrum while developing the model of an atom. We discuss the various postulates of the Bohr Atomic Model.

The Bohr model shows that the electrons in atoms are in orbits of differing energy around the nucleus. The electron in an atom has only certain definite stationary states of motion allowed to it, called as energy levels. Each energy level has a definite energy associated with it. In each of these energy levels, electrons move in circular orbit around the positive nucleus. The necessary centripetal force is provided by the electrostatic attraction of the protons in the nucleus. As one moves away from the nucleus, the energy of the levels increases.
The energy level occupied by an electron usually is called the ground state. It may move to a level of higher energy or a less stable shell by absorbing energy. This higher energy but less stable shell or level is termed as the excited state of the electron.
These states of allowed electronic motion are those in which the angular momentum of an electron is an integral multiple of h/2π or one can say that the angular momentum of an electron is quantized.

Angular Momentum

where m is the mass, v is the velocity, r is the radius of the orbit, h is Planck's constant and n is a positive integer.

Shells in a Atom

When an atom is in one of these states, it does not radiate any energy but whenever there is a transition from one state to other, energy is emitted or absorbed depending upon the nature of transition.

When an electron jumps from higher energy state to the lower energy state, it emits radiations in form of photons or quanta. However, when an electron moves from lower energy state to a higher state, energy is absorbed, again in form of photons.
After reaching the state of excitation, the electron can return to its original ground state by releasing the energy it has absorbed.
Sometimes the energy released by electrons occupies the portion of the electromagnetic spectrum (the range of wavelengths of energy) that humans detect as visible light. Slight variations in the amount of the energy are seen as light of different colors.
The energy of a photon emitted or absorbed is given by using Planck's relation (E = h $\nu$ ). If E₁be the energy of any lower energy state and E₂ be the energy of any higher energy state then the energy of the photon (emitted or absorbed) is given as ΔE:

Where h = Planck's constant and $\nu$ = frequency of radiation emitted or absorbed.

Though the Bohr postulates of atomic model worked quite well it has certain limitations. It is applicable only to one electron atoms like helium He⁺and lithium Li⁺⁺ apart from hydrogenH^- atom.

Energy Released in an Atom due to the Electron Jumping from one State to Another State

Here, we shall discuss the concept of Bohr’s orbits by defining the radius of orbits around the nucleus and the velocity and energy of an electron in various orbits around the nucleus.

We take the following assumptions:

r_n : radius of nth orbit

v_n : velocity of electron in nth state (orbit)

E_n : energy of nth state

m: mass of an electron (9.1 x 10^–31 Kg)

Z: atomic number (No. of Protons)

K = 1/(4πε₀) = constant = 9 x 10⁹ N m² C^–2

h: Planck's constant (6.67 x 10^–34 J-s)

c: velocity of light (3 x 10⁸ m/s)

R: Rydberg constant (1.097 x 10⁷ m^–1)

e: Charge on an electron (1.6 x 10^–19 C)

$\nu$ : frequency of the radiation emitted or absorbed

$\bar{\nu }$ : wave number of the spectral line in the atomic spectra

From Bohr’s first postulate,

mv² / r_n = KZe² / r_n²

FromBohr’s second postulate,

mv_nr_n = nh / 2π

Solving for rn and v_n, we have:

Radius,

= 0.53 × 10^–10 n²/Z m

= 0.53 n² / Z A

Velocity,

= (2.165 × 10⁶ Z/n) m/s

Energy of an electron in ‘n’ th state E_n :-

E_n = KE + PE

E_n = 1/2 mv² + (– KZe² / r_n) = –1/2 KZe² / r_n

=> E_n = –2π²K²e⁴Z² / n²h² (putting value of r_n)

= –2.178 × 10^–18 Z²/n² J / atom

= –13.6 Z2/n2 eV/atom

= –1312 Z²/n² kJ/mol

When an electron jumps from an outer orbit (higher energy) n₂ to an inner orbit (lower energy) n₁, then the energy emitted in form of radiation is given by:

$\Delta E= E_{n_{2}} = E_{n_{1}}$

= (2π²e⁴mZ²K²/h²) (1/n₁² – 1/n₂²)

As we know that E = h $\nu$ , c = $\nu$ λ and $\bar{\nu }$ =1/λ

So, $\bar{\nu }$ =?E/hc

$\bar{\nu }$ =1/λ= (2π²e⁴mZ²K²/ch³) (1/n₁² – 1/n₂²)

Now this can be represented as:

$\bar{\nu }$ ==RZ² (1/n₁² – 1/n₂²)

Where,

is the Rydberg’s constant.

Refer this vdeo to know more about on,”Bohr Model”:-

Energy Released in an Atom

Points to be noted:-

Bohr’s Theory was quite successful as it introduced various new concepts about atom. The relation given by Bohr resembles the empirical relation given by

Balmer& Rydberg on the spectral lines in H-atom spectra. The value of R as obtained above in the Bohr’s theory is the same as obtained in the empirical relation. Bohr’s atomic model postulates introduced various concepts like:

Bohr found that closer the electron to the nucleus the less energy it needs, while if it is far away from the nucleus it requires more energy. Because of this Bohr numbered the energy levels of electrons. If the energy level is high, farther is the electron from the nucleus.
He also found that there is a fixed number of electrons that every energy level can hold. The level 1 can hold up to 2 electrons, while the level 2 can hold up to 8 electrons and so on.

The only limitation with the Bohr’s model is that it works well for simple atoms like hydrogen but fails to good hold in more complex atoms. The quantum mechanical model is a better version of the Bohr model and is more frequently used today.

Problem (JEE Advanced):

In a hydrogen atom, the binding energy of the electron in the ground state is E₁. Find out the frequency of revolution of the electron in the n^th orbit.

Solution:

Numerically the binding energy is equal to the kinetic energy.

½ mv² = E₁ …....(1)

mvr = nh/2π …... (2)

Dividing equation (1) by equation (2), we get,

v/2πr = 2E₁/nh

Or, f = 2E₁/nh

Thus from the above observation we conclude that, the frequency of revolution of the electron in the n^th orbit would be 2E₁/nh.

For a particular orbit (n = constant) , orbital velocity of electron varies directly as the atomic number of the substance (vn∝Z).
For a particular element (Z= constant), orbital velocity of the lectron varies inversely as the order of the orbit.
Wavelength of emitted radiation depends upon the orders of two orbits between which the transition takes place.
For a particular transition radiation emitted by a heavier element possesses greater wave number and hence the smaller wavelength.
Electrons in the outer, electrons in higher elements are more energetic.
For a particular order, electrons in higher elements are less energetic.

Question 1

The atomic number of an atom identifies the number of

(a) protons

(b) neutrons

(d) excited states

Question 2

The Bohr model of the atom was able to explain the Balmer series because

(a) larger orbits required electrons to have more negative energy in order to match the angular momentum.

(b) differences between the energy levels of the orbits matched the difference between energy levels of the line spectra.

(d) none of the above.

Question 3

According to the equation de Broglie derived to describe matter waves, doubling the velocity of an electron would result in

(a) less momentum

(b) a greater mass

(d) an unchanged wavelength and mass

Question 4

One reason the Bohr model of the atom ultimately failed was because it did not explain why

(a) accelerating electrons do not emit electromagnetic radiation.

(b) moving electrons have a greater mass.

(d) electrons in greater orbits of an atom have greater velocities.

Q.1	Q.2	Q.3	Q.4
c	b	c	a

Related Resources:-

You might like to refer Energy Levels of Hydrogen Atom.
For getting an idea of the type of questions asked, refer the Previous Year Question Papers.
Click here to refer the most Useful Books of Physics.
To get answer to any question related to Bohr Model click here.