Solved Examples on Structure of Atom

Bohr's Theory of Atom and de-Broglie's Wavelength

Atoms are the basic building blocks of matter which has mass and occupies space. They cannot be chemically subdivided by ordinary means. The word ‘atom’ is derived from the Greek word atom which means indivisible. Matter can be broken into small particles called atoms which are too small to be seen through the naked eye.

As discussed earlier, atoms are composed of three types of particles namely protons, neutrons and electrons. A major proportion of mass of an atom is due to protons and neutrons while electrons have very small mass of about (9.108 X 10^-28 grams).Atoms are the basic unit of matter and it is vital to have a thorough knowledge of its components like electrons, protons and neutrons.

We have enlisted the information of various particles along with their charges in the table given below:

Particle	Charge	Mass (g)	Mass (amu)
Proton	+1	1.6727 x 10-24 g	1.007316
Neutron	0	1.6750 x 10-24 g	1.008701
Electron	-1	9.110 x 10-28 g	0.000549

We discuss some of the illustrations on the structure of an atom:

Problem 1:-

A doubly ionized Lithium atom is hydrogen like with atomic number 3.

(i) Find the wavelength of radiation required to excite the electron in Li⁺⁺ from the first to the third Bohr Orbit. (Ionization energy of the hydrogen atom equals 13.6 eV).

(ii) How many spectral lines are observed in the emission spectrum of the above excited system?

Solution:-

We are required to find the energy required to excite doubly ionized lithium. We know that,

E_n = –13.6 Z² / n²

Hence, the excitation energy = ΔE = E₃ – E₁ = –13.6 × (3)² [1/3² – 1/1²]

= +13.6 × (9) [1–1/9] = 13.6 × (9) (8/9) = 108.8 eV.

Wavelength λ = hc / ΔE = (6.63 × 10^–34) (3×10⁸) / (13.6 × 8) (1.6 × 10^–19)

= (6.63 × (3) / (13.6) (8)(1.16)) 10^–7

= 114.26 × 10–10 m

= 1143 A

(ii) From the excited state (E₃), coming back to ground state, there can be ³C₂ = 3 possible radiations.

_____________________________________________________________________________________________

Problem 2:-

Radiation emitted in the transition n = 3 to n = 2 orbit in a hydrogen atom falls on a metal to produce photoelectrons, the electrons emitted from the metal surface with the maximum kinetic energy are allowed to pass through a magnetic field of strength 3.125x10^-4 T and it is observed that the paths have radius of curvature as 10 mm. Find,

Electron Orbits Around in Different Shell in an Atom

(a) The kinetic energy of the fastest photo electrons.

(b) The work function of the metal.

Solution:-

First we discuss how to find the kinetic energy of the fastest photoelectron. The formula used for finding the same is

ΔE = hv₂₃ – 13.6 (1/2² – 1/3²) eV

The Kinetic energy of the fastest photoelectrons is given by

mv² / r = Bev

or mv = p = Ber

Kinetic Energy = 1/2 mv^2 = B²e²r² / 2m

= (3.125 × 10–4)2 × (1.6 ×)

= 0.86 eV

(a) The kinetic energy of the fastest electron is 0.86 eV

(b) The work function, Φ is given by

Φ = (1.9 – 0.86) eV = 1.04 eV

λ = hc/E = (6.63 × 10^–34) × (3×10^–8) / 1.3 × 1.6 × 1^–19 m

= 6.54 × 10^{–7 m}

= 6540Å

Orbital velocity of electron:

(a) it is smaller in outer orbits v_n = v₁/n.

(b) In a particular order it is greater for heavier elements.

Radius of orbit:

(a) It varies directly as square of order of orbit r∝n².

(b) For a particular order it is smaller for heavier elements.

Energy of electron:

(a) Electrons in the outer, electrons in higher elements are more energetic.

(b) For a particular order, electrons in higher elements are less energetic.

Wave number/wave length of emitted radiation:

(a) it depends upon the orders of two orbits between which the transition takes place.

(b) For a particular transition radiation emitted by a heavier element possesses greater wave number and hence the smaller wavelength.

Laymen series lies in ultraviolet region, Balmer series in visible region while Paschen, Bracket and P fund series lie in infrared region.
A line having longest wavelength, in a particular series, corresponds to the transition of electron from the nearest higher orbit.

Problem 3:-

Balmer Series of a Hydrogen Atom

Which electronic transition in Balmer series of hydrogen atom has same frequency as that of n = 6 to n = 4 transition in He⁺. [Neglect reduced mass effect].

Solution:-

v^-_He⁺ = RZ² [ 1/4² - 1/6²]

= 4R [ 36 - 16/36 x 16 ] = 5R/36

v^-_H= R x 1² [ 1/2² - 1/n²]

So, v^-_He⁺= v^-_H

5R/36 = R/4 - R/n²

On solving above equation

n² = 9

Thus, n = 3

Or corresponding transition from 3 → 2 in Balmer series of hydrogen atom has same frequency as that of 6 → 4 transition in He⁺.

_______________________________________________________________________________________________

Problem 4:-

Calculate ionization potential in volts of (a) He⁺ and (b) Li²⁺.

Solution:-

I.E. = 13.6Z²/n²

= 13.6 x Z² \1²[Z =2 for He⁺]

= 13.6 x 4 = 54.4 eV

Similarly for Li²⁺ = 13.6 x 3²/1²

= 13.6 x 9 = 122.4 eV

_________________________________________________________________________________________________________________

Problem 5:-

Calculate the ratio of K.E and P.E of an electron in an orbit?

Solution:-

K.E. = Ze²/2r

P.E. = -Ze²/r

So, P.E. = –2K.E

Thus, K.E/P.E = - ½

______________________________________________________________________________________________

Problem 6:-

How many spectral lines are emitted by atomic hydrogen excited to n^th energy level?

Solution:-

Spectral Lines of a Hydrogen Atom

Thus the number of lines emitted from nth energy level

= 1 + 2 + 3 +………… n – 1 = ∑(n – 1)

∑n = n(n+1)/2

Thus, ∑ (n – 1) = ( n-1) (n-1+1)/2 = (n-1) (n)/2

Number of spectral lines that appear in hydrogen spectrum when an electron jumps from n^thenergy level = n (n-1)/2

__________________________________________________________________________________________________

Problem 7:-

Calculate (a) the de Broglie wavelength of an electron moving with a velocity of 5.0x 10⁵ ms^–1 and (b) relative de Broglie wavelength of an atom of hydrogen and atom of oxygen moving with the same velocity (h = 6.63 x 10^–34 kg m² s^–1)

Solution:-

(a) λ = h/mv = 6.63 x 10^-34kgm2s^-2/ (9.11 x 10^-31kg) ( 5.0 x 10⁵ms^-1)

Wavelength λ = 1.46 x10^–9m

(b) An atom of oxygen has approximately 16 times the mass of an atom of hydrogen. In the formula λ = h/mv, h is constant while the conditions of problem make v, also constant. This means that λ and m are variables and λ varies inversely with m. Therefore, λ for the hydrogen atom would be 16 times greater than λ for oxygen atom.

____________________________________________________________________________________________

Problem 8:-

A 1 MeV proton is sent against a gold leaf (Z = 79). Calculate the distance of closest approach for head on collision.

Solution:-

K.E. = P.E.

1/2mv² = 1/4πε_o Ze²/d

Hence d = Ze²/4πε_o( 1/2mv²)

= 9 x 109 x 7⁹ x ( 1.6 x 10^-19)² / ( 1.6 x 10^-13 ) [ as 1 MeV = 1.6 x 10^-13 J]

= 1.137 x 10^-13 m

_______________________________________________________________________________________________

Problem 9:-

What is the wavelength associated with 150 eV electron

Solution:-

λ = h/√2 x m x K.E.

= 6.626 x 1^-34Js / √ 2 x 9.1 x 10^-31kg x 150 x 1.6 x 10^-19 J = 6.626 x 10^-34 / √4368 x 10^-50 = 10^–10 m = 1 Å

_____________________________________________________________________________________________

Problem 10:-

The energy of electron in the second and third Bohr orbit of the hydrogen atom is –5.42 x 10^–12erg and –2.41 x 10^–12erg, respectively. Calculate the wavelengths of emitted radiation when the electron drops from third to second orbit.

Solution:-

E₃ – E₂ = hv = hc/λ – 2.41 ´ 10^–12 – (– 5.42 ´ 10^–12) = 6.626 x 10^-27 x 3 x 10¹⁰/ λ

Thus, λ = 6.626 x 10^-27 x 3 x 10¹⁰ / 3.01 x 10^-12

= 6.604 x 10^–5 cm = 6.604 x 10^–5 x 10⁸ = 6604 Å

________________________________________________________________________________________________

Problem 11:-

Compare the wavelengths for the first three lines in the Balmer series with those which arise from similar transition in Be³⁺ ion. (Neglect reduced mass effect).

Solution:-

v^-_H = R x 1² ( 1/2² - 1/n²)

v^-_Be = R x 4² ( 1/2² - 1/n²)

Thus, v^-_Be/v^-_H = λ_H / λ_Be = 16

So we can conclude that all transitions in Be³⁺ will occur at wavelengths 1/16 times the hydrogen wavelengths.

View this video for more examples on structure of atom:

Problem 12:-

Find the ratio of de-Broglie wavelength of molecules of hydrogen and helium in two gas jars kept separately at temperature 27ºC nad 127ºC respectively.

Solution:-

We know that, de-Broglie wavelength λ = h/mv.

where the speed (r.m.s) of a gas particle at the given temperature (T) is given as,

½ mv² = 3/2 KT

or, v = √ 3kT/m

Here K is Boltzmann’s constant, m is mass of the gas particle and T is the temperature of gas in K.

So, mv = √3mKT

or, λ = h/mv = h/√3mKT

Thus, λ_H/λ_He = √ m_HeT_He/m_HeT_H = √ (4 amu) (273+127º)K / (2 amu) (273+27º)K = √8/3

_________________________________________________________________________________________________

Problem 13:-

A single electron orbits a stationary nucleus of charge Ze where Z is a constant and e is the electronic charge. It requires 47.2 eV to excite the electron from the 2^nd bohr orbit to 3^rd Bohr orbit. Find

(a) the value of Z

(b) energy required to excite the electron from the third to the fourth orbit.

(d) the kinetic energy, potential energy and angular momentum in the first Bohr orbit.

(e) the radius of the first Bohr orbit.

Solution:-

We can find difference of eneregy of n = 2 and n = 3 as E₃ – E₂ = 47.2

(13.6) z² [1/4 – 1/9] = 47.2

z = 5

Energy required to excite from n = 3 to n = 4, 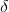$\Delta$ E = E₄ – E₃ = (13.6) (5)² [1/9 – 1/16] = 16.5 ev

Ionization energy = 13.6 (z)² = 13.6 (5)⁵ = 340 eV

Corresponding wavelength of photon = (12400/340) Å = 36.5 Å

In first Bohr orbit: (n = 1)

KE₁ = 340 eV

PE₁ = -680 eV

E₁ = -340 eV

Radius of first Bohr orbit, r₁ = (0.53) n²/z = 0.53/5 = 0.106 Å

Question 1:-

If the wave properties of a particle are difficult to observe, it is probably due to the particle's

(a) small size

(b) large mass

(d) high charge

Question 2:-

The energy of a photon varies directly with its

(a) frequency

(b) wavelength

(d) rest mass

Question 3:-

Which color of light has the greatest energy per photon?

(a) blue

(b) green

(d) red

Question 4:-

Linear momentum of a photon is

(a) zero (b) hν/c²(c) hν/c (d) c²/hν

Question 5:-

Stopping potential for a metal surface in case of photoelectric emission depends on

(a) the threshold frequency for the metal surface

(b) the intensity of incident light

(d) all of the above

Q.1	Q.2	Q.3	Q.4	Q.5
b	a	c	a	c

Related Resources:-

You might like to refer Bohr model.
For getting an idea of the type of questions asked, refer the Previous Year Question Papers.
Click here to refer the most Useful Books of Physics.