Objective Questions of Thermodynamics and Answers with Explanation:-

Problem 1:-

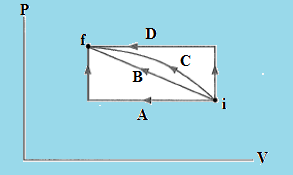
In which of the paths between initial state i and final state f in the below figure is the work done on the gas the greatest?

Path Between Initial State and Final State in a P-V diagram Solution:-

The correct option is (D).

Work is a path function. So work done on the gas depends upon the path. The area under pv diagram gives the work done on the gas between initial state i and final state f. As the area under the path D is greater than the other path, therefore the paths between initial state i and final state f where the work done on the gas is greatest would be D. From the above observation we conclude that, option D is correct.

_____________________________________________________________________

Problem 2:-

A 1-kg block of ice at 0ºC is placed into a perfectly insulated, sealed container that has 2 kg of water also at 0ºC. The water and ice completely fill the container, but the container is flexible. After some time one can except that

(A) the water will freeze so that the mass of the ice will increase.

(B) the ice will melt so that the mass of the ice will decrease.

(D) both the amount of water and the amount of ice will decrease.

Solution:-

The correct option is (B) the ice will melt so that the mass of the ice will decrease.

In accordance to second law of thermodynamics, if an irreversible process occurs in a closed system, the entropy of that system always increases; it never decreases. Entropy measures the state of disorder. As the ice is more order than water, therefore the ice will melt so that the mass of the ice will decrease. From the above observation we conclude that, option (B) is correct.

________________________________________________________________________________

Problem 3:-

Which of the following processes must violate the first law of thermodynamics? (There may be more than one answer!)

(A) W > 0, Q < 0, and ?E_int = 0

(B) W > 0, Q < 0, and ?E_int > 0

(D) W < 0, Q > 0, and ?E_int < 0

(E) W > 0, Q > 0, and ?E_int < 0

Solution:-

The correct option is (E).

In accordance to first law of thermodynamics, for a thermodynamic system, in which internal energy is the only type of energy the system may have, the law of conservation of energy may be expressed as

Q + W = ΔE_int

Here Q is the energy transferred (as heat) between the system and environment, W is the work done on (or by) the system and ΔE_int is the change in the internal energy of the system.

By convention we have chosen Q to be positive when heat is transferred into the system and W to be positive when work is done on the system.

In the option (E), W > 0 and Q > 0. If we put this condition in the left hand side of the equation Q + W = ΔE_int, then the right hand side of the equation must be greater than zero (ΔE_int > 0). Thus W > 0, Q > 0, and ΔE_int < 0 must violate the first law of thermodynamics. Therefore option (E) is correct.

________________________________________________________________________________

Problem 4:-

A spherical constant temperature heat source of radius r₁ is at the center of a uniform solid sphere of radius r₂. The rate at which heat is transferred through the surface of the sphere is propertional to

(A) r₂² – r₁²

(B) r₂ – r₁

(D) 1/r₂ – 1/r₁

(E) (1/r₂ – 1/r₁)^-1

Solution:-

The correct option is (A).

The rate H at which heat is transferred through the slab is,

(a) directly proportional to the area (A) available.

(b) inversely proportional to the thickness of the slab Δx.

So, H = kA ΔT/ Δx

Where k is the proportionality constant and is called thermal conductivity of the material.

From above we know that, the rate H at which heat is transferred through the slab is directly proportional to the area (A) available.

Area A of solid sphere is defined as,

A = 4πr²

Here r is the radius of sphere.

So, the area A₁ of uniform small solid sphere having radius r₁ will be,

A₁ = 4πr₁²

And, the area A₂ of uniform large solid sphere having radius r₂ will be,

A₂ = 4πr₂²

Thus the area A from which heat is transferred through the surface of the sphere will be the difference of area of uniform large solid sphere A₂ and small solid sphere A₁.

So, A = A₂ - A₁= 4πr₂² - 4πr₁²= 4π (r₂² - r₁²)

Since the rate H at which heat is transferred through the slab is directly proportional to the area (A) available, therefore the rate at which heat is transferred through the surface of the sphere is proportional to r₂² - r₁².

From the above observation we conclude that, option (A) is correct.

____________________________________________________________________________________

Problem 5:-

What would be the most likely value for C_T, the molar heat capacity at constant temperature?

(A) 0

(B) 0 < C_T < C_v

(D) C_T = $\infty$

Solution:-

The correct option is (A).

Molar heat capacity at constant temperature (C_T) is defined as the amount of heat required to raise the temperature of 1 g of gas through 1° C keeping its temperature constant. But it is impossible to rise the temperature of 1 g of gas through 1° C keeping its temperature constant. So the two statements contradict to each other. Thus the most likely value for molar heat capacity at constant temperature (C_T) will be zero. Therefore option (A) is correct.

_______________________________________________________________________________________---

Problem 6:-

Which type of ideal gas will have the largest value for C_p – C_v?

(A) Monoatomic

(B) Diatomic

(D) The value will be the same for all.

Solution:-

The correct option is (D).

The specific heat at constant volume (C_v) for monoatomic gas is,

C_v = 3/2 R

The specific heat at constant volume (C_v) for diatomic gas is,

C_v = 5/2 R

The specific heat at constant volume (C_v) for polyatomic gas is,

C_v = 3 R

But we know that, for an ideal gas,

C_p - C_v = R

So,the specific heat at constant pressure (C_p) for monoatomic gas will be,

C_p = C_v + R = 3/2 R + R = 5/2 R

the specific heat at constant pressure (C_p) for diatomic gas will be,

C_p = C_v + R = 5/2 R + R = 7/2 R

the specific heat at constant pressure (C_p) for polyatomic gas will be,

C_p = C_v + R = 3 R + R = 4 R

Therefore,

C_p - C_v for monoatomic gas will be,

C_p - C_v = 5/2 R - 3/2 R = R

C_p - C_v fo diatomic gas will be,

C_p - C_v = 7/2 R - 5/2 R = R

C_p - C_v fo polyatomic gas will be,

C_p - C_v = 4 R - 3 R = R

From the above observation we conclude that, the value of C_p - C_v will be same for all ideal gas. Therefore option (D) is correct.

__________________________________________________________________________________________________

Problem 7:-

Consider the following processes that can be done on an ideal gas: constant volume, ΔV = 0; constant pressure, Δp = 0; and constant temperature, ΔT = 0.

(a) For which process does W = 0?

(b) For which process does Q = 0?

(d) For which of these process does ΔE_int = Q?

(e) For which of these process does ΔE_int = W?

(A) ΔV = 0 (B) Δp = 0 (C) ΔT = 0 (D) None of these

Solution:-

(a) The correct option is (A) ΔV = 0.

The change in work done ΔW is defined as,

ΔW = pΔV

Therefore W = 0 for the process where ΔV = 0. From the above observation we conclude that, option (A) is correct.

(b) The correct option is (D) None of these.

In adiabatic process the exchange of heat with surrounding is zero (Q=0). In this process, the change of volume, pressure and temperature occurs. Therefore option (D) is correct.

For a thermodynamic system, in which internal energy is the only type of energy the system may have, the law of conservation of energy may be expressed as,

Q + W = ΔE_int

Here Q is the energy transferred (as heat) between the system and its environment, W is the work done on or by the system and ΔE_int is the change in the internal energy of the system.

As W + Q = 0, it signifies that ΔE_int = 0 and it is possible only when ΔT = 0. Therefor option (C) is correct.

(d) The correct option is (A) ΔV = 0.

For a thermodynamic system, in which internal energy is the only type of energy the system may have, the law of conservation of energy may be expressed as,

Q + W = ΔE_int

Here Q is the energy transferred (as heat) between the system and its environment, W is the work done on or by the system and ΔE_int is the change in the internal energy of the system.

As ΔE_int = Q, it signifies that W=0.

The change in work done ΔW is defined as,

ΔW = pΔV

Therefore W = 0 for the process where ΔV = 0. From the above observation we conclude that, option (A) is correct.

(e) The correct option is (D) None of these.

For a thermodynamic system, in which internal energy is the only type of energy the system may have, the law of conservation of energy may be expressed as,

Q + W = ΔE_int

Here Q is the energy transferred (as heat) between the system and its environment, W is the work done on or by the system and ΔE_int is the change in the internal energy of the system.

As ΔE_int = W, it signifies that Q=0.

In adiabatic process the exchange of heat with surrounding is zero (Q=0). In this process, the change of volume, pressure and temperature occurs. Therefore option (D) is correct.

_________________________________________________________________________________________

Problem 8:-

Consider an ideal heat pump and a perfect electric heater. The electric heater converts 100% of the electrical energy into heat energy; the heat pump converts 100% of the electrical energy into work, which then powers a Carnot refrigerator. Which is the more “efficient” way to heat a home? (Ignore maintenance or start-up costs.)

(A) The electric heater is always more efficient.

(B) The heat pump is always more efficient.

(D) The heat pump is more efficient if the outside temperature is not too cold.

Solution:-

The correct option is (C).

A heat pump is a device that acting as a Carnot refrigerator can heat a house by transferring heat energy from the outside to the inside of the house; the process is driven by work done on the device. So, heat pump, which is also a refrigerator, is an air conditioner that can be operated in reverse to heat room. By heating the room using a perfect electric heater, there is some loss of thermal energy due to heating the coil of the electric heater.

The value of coefficient of performance K becomes larger as the temperature of the two reservoirs becomes more nearly the same. Thus heat pumps are more efficient in temperate climates than in climates where the outside temperature fluctuates between wide limits. From the above observation we conclude that, the heat pump is more efficient if the outside temperature is not too warm. Thus option (C) is correct.

______________________________________________________________________________________________

Problem 9:-

A real engine operates at 75% of the efficiency of a Carnot engine operating betwen the same two temperatures. This engine has a power output of 100 W and discharges heat into the 27ºC low-temperature reservior at a rate of 300 J/s. what is the temperature of the high-temperature reservior?

(A) 27ºC (B) 77ºC (C) 127ºC (D) 177ºC

Solution:-

The correct option is (C) 127^° C.

The efficiency ε of a Carnot engine is defined as,

ε = |Q_H| -|Q_L|/|Q_H|

=1- |Q_L|/|Q_H|

= 1- T_L/T_H

Here Q_L is the heat at lower temperature, Q_H is the heat at higher temperature, T_L is the lower temperature and T_H is the higher temperature.

As the real engine has a power output of 100 W (100 J/s) and discharge heat into the 27^° C low-temperature reservoir at a rate of 300 J/s.

Here, |Q_H| -|Q_L| = 100 J

And

|Q_L| = 300 J

So, |Q_H| -300 J = 100 J

|Q_H| = 400 J

To obtain the efficiency ε of this real engine, substitute 300 J for Q_L and 400 J for Q_H in the equation ε = 1- |Q_L/Q_H|,

ε = 1- |Q_L/Q_H|

= 1-300 J/400 J

= 1/4

To obtain the temperature of the high-temperature region T_H, substitute 1/4 for ε, 27^° C for T_L in the equation ε =1- T_L/T_H we get,

1/4=1- T_L/T_H

= 1-27^° C/ T_H

= 1- (27+273) K/ T_H

= 1- 300 K/ T_H

So,300 K/ T_H = ¾

T_H= 400 K

= (400 -273)^° C

= 127 ^° C

Therefore the temperature of the high-temperature region T_H would be 127 ^° C. From the above observation we conclude that, option (C) is correct.

___________________________________________________________________________________________

Problem 10:-

A real has an efficiency of 33%. The engine has a work output of 24 J per cycle.

(a) How much heat energy is extracted from the high temperature reservior per cycle?

(A) 8 J (B) 16 J (C) 48 J (D) 72 J (E) The question can be answered only if the engine is a carnot engine

(b) How much heat energy is discharged into the low-temperature reservior per cycle?

(A) 8 J (B) 16 J (C) 48 J (D) 72 J (E) The question can be answered only if the engine is a carnot engine

(A) T_H = 450ºC (B) T_H = 177ºC

(E) 177ºC < T_H < 450ºC

Solution:-

(a) The correct option is (D) 72 J.

The efficiency ε of a Carnot engine is defined as,

ε = |Q_H| -|Q_L|/|Q_H|

=1- |Q_L|/|Q_H|

= 1- T_L/T_H

Here Q_L is the heat at lower temperature, Q_H is the heat at higher temperature, T_L is the lower temperature and T_H is the higher temperature.

As, ε = |Q_H| -|Q_L|/|Q_H|

= ΔW/|Q_H| (Since, |Q_H| -|Q_L| = ΔW)

To obtain the amount of heat energy is extracted from the higher temperature |Q_H|, substitute 33% for ε and 24 J for ΔW in the equation ε = ΔW/|Q_H|, we get,

ε = ΔW/|Q_H|

33/100 = 24 J/|Q_H|

Or, |Q_H| = (2400/33) J

= 72.73 J

Rounding off to two significant figures, the amount of heat energy is extracted from the higher temperature |Q_H| would be 72 J. From the above observation we conclude that, option (D) is correct.

(b) The correct option is (C) 48 J.

To obtain the heat energy is discharged into the low-temperature reservoir per cycle |Q_L|, substitute 72 J for |Q_H| and 33% for ε in the equation ε =1- |Q_L|/|Q_H|,

ε =1- |Q_L|/|Q_H|

33/100 = 1-|Q_L|/72 J

|Q_L|/72 J = 1-33/100

= 67/100

So,|Q_L| = (67/100)×72 J

= 48.24 J

Rounding off to two significant figures, the heat energy is discharged into the low-temperature reservoir per cycle |Q_L| would be 48 J. From the above observation we conclude that, option (C) is correct.

To obtain T_H, substitute 33% for ε, 27^° C for T_L in the equation ε =1- T_L/T_H we get,

33/100 =1- T_L/T_H

= 1-27^° C/ T_H

27^° C/ T_H =1-33/100

=67/100

T_H =27^° C×100/67

=40.30^° C

<177^° C

Therefore the value of T_H will be <177^° C. From the above observation we conclude that, option (D) is correct.

__________________________________________________________________________________

Problem 11:-

A Carnot engine discharges 3 J of heat into the low temperature reservior for every 2 J of work output.

(a) What is the efficiency of this Carnot engine?

(A) 1/3 (B) 2/5 (C) 3/5 (D) 2/3

(b) For this engine T_L = 27ºC, What can be concluded about T_H?

(A) T_H = 627ºC (B) T_H = 227ºC

(E) 227ºC < T_H < 627ºC

Solution:-

(a) The correct option is (A) 1/3.

The efficiency ε of a Carnot engine is defined as,

ε = 1- |Q_L/Q_H|

= 1- T_L/T_H

Here Q_L is the heat at lower temperature, Q_H is the heat at higher temperature, T_L is the lower temperature and T_H is the higher temperature.

To obtain the efficiency ε of this Carnot engine, substitute 2 J for Q_L and 3 J for Q_H in the equation ε = 1- |Q_L/Q_H|,

ε = 1- |Q_L/Q_H|

= 1-2 J/3 J

= 1/3

Thus the efficiency of this Carnot engine would be 1/3. From the above observation we conclude that, option (A) is correct.

(b) The correct option is (D) T_H <227^° C.

The efficiency ε of a Carnot engine is defined as,

ε = 1- |Q_L/Q_H|

= 1- T_L/T_H

Here Q_L is the heat at lower temperature, Q_H is the heat at higher temperature, T_L is the lower temperature and T_H is the higher temperature.

To obtain the efficiency ε of this Carnot engine, substitute 2 J for Q_L and 3 J for Q_H in the equation ε = 1- |Q_L/Q_H|,

ε = 1- |Q_L/Q_H|

= 1-2 J/3 J

= 1/3

Thus the efficiency of this Carnot engine would be 1/3.

To obtain T_H, substitute 1/3 for ε, 27^° C for T_L in the equation ε =1- T_L/T_H we get,

1/3=1- T_L/T_H

= 1-27^° C/ T_H

T_H = 27^° C×3/2

=40.5^° C

<227^° C

Therefore the value of T_H will be <227^° C. From the above observation we conclude that, option (D) is correct.

___________________________________________________________________________________

Problem 12:-

Which of the following is a consequence of the second law of thermodynamics?

(A) Heat can flow only from high temperature to low temperature.

(B) Objects in contact will tend toweard having the same temperature.

Solution:-

The correct option is (C).

In accordance to second law of thermodynamics, when changes occur due to external influence within a closed system its entropy either increases (for irreversible process) or remains constant (for reversible process). It never decreases. Entropy is often associated with disorder and the second law of thermodynamics is sometimes cast as a statement that the disorder of a closed system always increases. The final state, with the randomly directed motions of its molecules, is more disorder than the initial state, with the directed motions of a substantially large number of its molecules. Thus any system that produces order from disorder must have an external influence. Therefore option (C) is correct.

______________________________________________________________________________________________

Problem 13:-

A block of aluminum originally at 80º C is placed into an insulated container of water originally at 25ºC. After a while the system reaches an equilibrium temperature of 31ºC.

(a) During the process

(A) ΔS_aluminum > 0 (B) ΔS_aluminum (C) ΔS_aluminum < 0

(b) During this process

(A) ΔS_water > 0 (B) ΔS_water = 0 (C) ΔS_water < 0

(A) |ΔS_water| > |ΔS_aluminum|

(B) |ΔS_water| = |ΔS_aluminum|

Solution:-

(a) The correct option is (C) ΔS_aluminum<0.

Entropy change (ΔS) for a reversible process is defined as,

ΔS = ΔQ/T

Where, ΔQ is the change in heat energy that is transferred into or out of the closed system at constant temperature T.

Whenever an irreversible process takes place, certain amount of energy which could have been utilized for doing useful work changes to a form in which it becomes unavailable. Entropy is a measure of disorder. Thus with disorder, entropy increases. The initial temperature of the aluminum block is 80^°C. But after some time the system reaches an equilibrium temperature of 31^°C. Therefore the aluminum block will colder than its original state. This signifies that, the change in entropy of the block of aluminum will be less than zero (ΔS_aluminum<0). From the above observation we conclude that option (C) is correct.

(b) The correct option is (A) ΔS_water>0.

Entropy change (ΔS) for a reversible process is defined as,

ΔS = ΔQ/T

Where, ΔQ is the change in heat energy that is transferred into or out of the closed system at constant temperature T.

Whenever an irreversible process takes place, certain amount of energy which could have been utilized for doing useful work changes to a form in which it becomes unavailable. Entropy is a measure of disorder. Thus with disorder, entropy increases. The initial temperature of water is 25° C. But after some time the system reaches an equilibrium temperature of 31^°C. Therefore the water will be much hotter than its original state. This signifies that, the change in entropy of the water will be greater than zero (ΔS_water>0). From the above observation we conclude that option (A) is correct.

(c) The correct option is (A) |ΔS_water| > | ΔS_aluminum|

In accordance to second law of thermodynamics, when changes occur within a closed system its entropy increases for an irreversible process. To satisfy the second law of thermodynamics in the system, the net change in entropy of water must be greater than the net change in entropy of aluminum (|ΔS_water| > | ΔS_aluminum|). From the above observation we conclude that, option (A) is correct.

_________________________________________________________________________________

Problem 14:-

For which of the following process is the entropy change zero?

(A) Isobaric (B) Isothermal

(E) None of these, since ΔS > 0 for all process.

Solution:-

The correct option is (C) adiabatic.

Entropy change (ΔS) for a reversible process is defined as,

ΔS = ΔQ/T

Where, ΔQ is the change in heat energy that is transferred into or out of the closed system at constant temperature T.

From equation ΔS = ΔQ/T, the entropy change will be zero when

ΔQ/T = 0

If the above condition is satisfied, ΔQ =0 as T is constant.

This shows that the change in the entropy is constant.

So, the process will be adiabatic process as the amount of heat remains constant. Thus in an adiabatic process the entropy change will be zero. Therefore option (C) is correct.

_____________________________________________________________________________

Problem 15:-

Ten identical particles are to be divided up into two containers.

(a) How many microstates belong to the configuration of three particles in one container and seven in the other?

(A) 120 (B) 30240 (C) 3628800 (D) 6.3 $\times$ 10⁹

(b) How many different configuration are possible?

(A) 1 (B) 11 (C) 120 (D) 1024 (E) 3628800

(d) Which configuration has the largest number of microstates?

(A) 0, 10 (B) 3, 7 (C) 4,6 (D) 5, 5

Solution:-

(a) The correct option is (A) 120.

The number of microstates that lead to a given configuration the multiplicity w of that configuration is defined as,

w = N!/N₁! N₂!

Here N = 10, N₁ = 3 and N₂ = 7.

So, w = N!/N₁! N₂!

= 10!/3! 7!

= 120

From the above observation we conclude that, the microstates belong to the configuration of three particles in one container and seven in other will be 120. Therefore option (A) is correct.

(b) The correct option is (E).

Ten identical particles are to be divided up into two containers. The total number of possible different configuration will be equal to N!.

Here N is the total number of particles.

As N = 10, N! = 10! = 3628800

From the above observation we conclude that, 3628800 different configuration are possible. Therefore option (E) is correct.

Ten identical particles are to be divided up into two containers. The total number of microstates for the ten particle system will be equal to 2^N.

Here N is the total number of particles.

As N = 10, 2^N = 2¹⁰ = 1024

From the above observation we conclude that, the total number of microstates for the ten particle system will be 1024. Therefore option (D) is correct.

(d) The correct option is (D).

The number of microstates that lead to a given configuration the multiplicity w of that configuration is defined as,

w = N!/N₁! N₂!

In the configuration (0,10) , N = 10, N₁ = 0 and N₂ = 10.

So, w = N!/N₁! N₂! = 10!/0! 10! = 1

In the configuration (3,7) , N = 10, N₁ = 3 and N₂ = 7.

So, w = N!/N₁! N₂! = 10!/3! 7! = 120

In the configuration (4,6) , N = 10, N₁ = 4 and N₂ = 6.

So, w = N!/N₁! N₂! = 10!/4! 6! = 210

In the configuration (5,5) , N = 10, N₁ = 5 and N₂ = 5.

So, w = N!/N₁! N₂! = 10!/5! 5! = 252

From the above observation we conclude that, the configuration which has the largest number of microstates will be (5,5). Therefore option (D) is correct.

Question 1:-

A system is taken from state A to state B along two different paths 1 and 2. The heat absorbed and work done by the system along these paths are Q₁ and Q₂ and W₁ and W₂respectively. Then

(A) Q₁ = Q₂

(B) W₁ + Q₁ = Q₂ + W₂

(D) Q₁ - W₁ = Q₂ - W₂

Question 2:-

When the gas expands under adiabatic condition, its temperature:

(a) increases

(b) decreases

(d) none of the above

Question 3:-

In a reversible adiabatic change ΔS is

(A) infinity

(B) zero

(D) equal to nRln V₂/V₁

Question 4:-

If the temperature of source increases, the efficiency of a Carnot’s engine:

(A) decreases

(B) increases

(D) may increase or decrease

Question 5:-

If the temperature of the sink is decreased, the efficiency of a Carnot engine:

(A) decreases

(B) increases

(D) first increase and then decrease

Question 6:-

Heat cannot flow by itself from a colder body to hotter body is a statement of:

(A) 2^nd law of thermodynamics

(B) conservation of momentum

(d) first law of thermodynamics

Q.1	Q.2	Q.3	Q.4	Q.5	Q.6
D	B	B	B	B	A

Related Resources:-

You might like to refer Solved problems on specific heat, latent heat and entropy.
For getting an idea of the type of questions asked, refer the Previous Year Question Papers.
Click here to refer the most Useful Books of Physics.

To read more, Buy study materials of Thermodynamics comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Chemistry here.

View courses by askIITians

Design classes One-on-One in your own way with Top IITians/Medical Professionals

Click Here Know More

Ask a Doubt

Get your questions answered by the expert for free

Enter text here...

Book a Live class Live courses Ask question

Objective Questions of Thermodynamics and Answers with Explanation:-

Problem 1:-

Problem 2:-

Solution:-

Problem 3:-

Solution:-

Problem 4:-

Solution:-

Problem 5:-

Solution:-

Problem 6:-

Solution:-

Problem 7:-

Solution:-

Problem 8:-

Solution:-

Problem 9:-

Solution:-

Problem 10:-

Solution:-

Problem 11:-

Solution:-

Problem 12:-

Solution:-

Problem 13:-

Solution:-

Problem 14:-

Solution:-

Problem 15:-

Solution:-

Question 1:-

Question 2:-

Question 3:-

Question 4:-

Question 5:-

Question 6:-

Related Resources:-

View courses by askIITians

Design classes One-on-One in your own way with Top IITians/Medical Professionals

Complete Self Study Package designed by Industry Leading Experts

Live 1-1 coding classes to unleash the Creator in your Child

a Complete All-in-One Study package Fully Loaded inside a Tablet!

Ask a Doubt