Wave Nature of Light

 

Table of Content

Huygens  Wave Theory Huygen’s Principle Construction of Wave Front Related Resources

Huygens  Wave Theory

Huygen, a Dutch mathematician, in 1678, gave a theory regarding nature of light. The theory is popularly known as Huygen’s wave theory. According to this theory, light is a sort of disturbance. The particles of the medium, vibrate in a direction, at right angle to the direction of propagation of disturbance. The process is called wave motion. Considering light to be a wave-motion following properties of light could be explained:

(a) Rectilinear propagation of light (b) Reflection (c) Refraction (d) Interference (e) Diffraction (f) Polarisation

Photoelectric effect could not be explained on the basis of this theory. A more serious objection to this theory was regarding the nature of medium, through which the light travels while coming from sun to earth, since major portion of space in between has vacuum. This hurdle was overcome by proposing a hypothetical medium ‘ether’. the properties of ‘ether’ as imagined by the supporters of this theory are self-contradicting. Moreover any attempt to test the presence of this medium has not been successful. The theory was, later on, modified by Max Planck by saying that the source of light does not give out continuous disturbance. Instead, it emits certain packets of energy consisting of vibratory energy. The modified theory is called Planck’s quantum theory and the packet of energy is treated to be the fundamental particle of light known as photon.
 

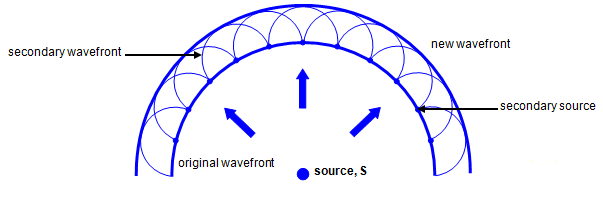
Huygen’s Principle

The following constructions were proposed by Huygen's to explain the wave propagation of light.

Primary source – The geometrical center or axis of the actual source of light which is either a point or a line is called the primary source.

Wavelets –  All points lying on small curved surfaces, that receive light at the same time from the same source (primary or secondary) are called wavelets.

Secondary source – Any point on a wavelet, acts as the source of light for further propagation of light. It is called a secondary source.

Wave front – The envelope of all wavelets in the same phase- having received light from sources in the same phase at the same time is called a wave front.

Wave normal – The normal at any point drawn outward on a wave front is called the wave normal. Further propagation of light occurs along the wave normal. In isotropic media the wave normal coincides with the 'ray of light'.

Spherical, cylindrical and plane wave fronts

The wave fronts from a point of the primary source are spherical wave fronts. The wave fronts from the line primary source are cylindrical wave fronts.

At large distances from the primary source the radius of curvature of the wave fronts is negligibly small. Small portions of such wave points are essentially flat or plane. These are called plane wave fronts.

Construction of Wave Front

Wave-front of a wave, at any instant, is defined as the locus of all the particles in the medium which are being disturbed at the same instant of time and are in the same phase of vibration.

How to construct a wave-front at any instant (say t + dt) if a wave-front at a slightly earlier instant (t) is known?

The answer is that Huygen’s principle gives us the guide lines to do so. Steps to be followed, in this process, are called the basic postulates of the principle and they are stated below.

(a) Consider all the points on a primary wave-front (of instant ‘t’) to be the sources of light, which emit disturbances known as secondary disturbance.

(b) Tangent envelope to all the secondary wave-lets gives the position of a new wave-front.

Consider a point source ‘S’. Light emitted by ‘S’ travels in all directions. Let AB be a section of the position of wave-front, at any instant, of time ‘t’ as shown in figure. The secondary disturbances emitted by all the points on AB are shown by dotted circles. A₁B₁ and A₂B₂ are the two tangent envelopes touching all these secondary disturbances.

According to Stoke’s law, the intensity at each point of the secondary wave is proportional to (1 + cosθ). Here ‘θ’ is angle between normal and central line.

For backward wave-front ‘A₂B₂’ (shown dotted), θ = π

So, cosθ = cosπ = -1

Thus, intensity at any point on backward wave = k (1+cosπ) = k (1-1) = 0

Therefore back wave-front does not exist.

Hence, ‘A₁B₁’ which is the forward wave-front gives the position of wave-front at the later instant.

Every point on a wave-front may be considered a source of secondary spherical wavelets which spread out in the forward direction at the speed of light. The new wave-front is the tangential surface to all of these secondary wavelets.

Straight wave front

Huygens's principle applied to a straight wave front. Each point on the wave front emits a semicircular wavelet that moves a distance s=vt. The new wavefront is a line tangent to the wavelets.

Huygen’s Refraction

Huygens's principle applied to a straight wavefront traveling from one medium to another where its speed is less. The ray bends toward the perpendicular, since the wavelets have a lower speed in the second medium.

Huygen’s Reflection

Huygens's principle applied to a straight wave front striking a mirror. The wavelets shown were emitted as each point on the wave front struck the mirror. The tangent to these wavelets shows that the new wave front has been reflected at an angle equal to the incident angle. The direction of propagation is perpendicular to the wave front, as shown by the downward-pointing arrows.
 

Watch this Video for more reference
 

Diffraction is the concept that is explained using Huygens's Principle, and is defined as the bending of a wave around the edges of an opening or an obstacle. This principal can be used to define reflection, as shown in the figure. It can also be used to explain refraction and interference. Anything the experiences this phenomenon is a wave. By applying this therory to light passing through a slit, we can prove it is a wave. From Huygen's construction we learn that while the medium is homogeneous (i.e., optical properties of the medium are same everywhere) light moves forward and does not reflect back. We also assume that the secondary wavelets are emitted only in forward direction i.e., in the direction of advancement of the wave. If there is a sudden obstruction or charge in medium as discussed below, the wave may be reflected from the discontinuity. The secondary wavelets on the backward side should also be considered.

Problem (JEE Advanced):

Two waves of same frequency and same amplitude from two monochromatic sources are allowed to suppose at a certain point. If in one case the phase difference is 0º and in other case is  π/2. Then find the ratio of the intensities in the two cases.

Solution:

As, A₁ = 2A

So, I₁ = 4I

A₂ = √2A

Thus, I₂ = 2I

Therefore, I₁/I₂ = 2/1

Thus from the above observation we conclude that, the ratio of the intensities in the two cases would be 2/1.

Drawbacks

• Many phenomena in Modern Physics such as Photo-electric effect, Compton effect, etc. could not be explained by wave theory.

• The propagation of waves through vacuum could not be accounted for, hence a hypothetical medium called ether was assumed to be present. However, the presence of ether could not be detected. It was experimentally shown that medium like ether does not exist.

Q.1	Q.2	Q.3	Q.4	Q.5
c	c	a	c	d

Related Resources

• You might like to Young’s Double slit Experiment.

• For getting an idea of the type of questions asked, refer the  Previous Year Question Papers.

• Click here to refer the most Useful Books of Physics.

• To get answer to any question related to wave nature of light click here.