Argand Plane and Polar Representation

 

Table of Content

What is an Argand Plane? How do you graph a Complex Number? What are the different forms of representation of Complex Number? Explain Polar representation in detail. Is Infinity imaginary number? What is a Complex Number plane? Explain Demoivre’s Theorem Application of Demoivre’s Theorem

What is an Argand Plane?

We are already aware of the Cartesian or xy – plane or Z - plane, which is used to represent any pair of point graphically. It has two mutually perpendicular axis namely x – axis and the y – axis. So any ordered pair (x, y) can be carefully located on this xy – plane. This Cartesian plane is used to locate any pair of real numbered points.

Argand plane is also the xy – plane or the Cartesian plane but here we consider x – axis as the real axis and y – axis as the imaginary axis. And thus argand plane is used to locate the complex numbers graphically.

Any complex number of the form z = a + ib can be treated as the ordered pair (a, b) and accordingly it can be represented on the argand plane.

Example Let z = 2 + 3i,

So we have Re(z) = 2 and Im(z) = 3. 

The distance of the any point from the origin is called as its Modulus and is represented by |z| for any complex number z.

If the complex number is purely real number i.e. its imaginary part is zero (b = 0), then on the argand plane it will be purely located on the real axis either towards right or left of the origin depending upon the sign of the number. That is, any point on the real axis will be of the form z = a + i0.

While for purely imaginary number i.e. its real part is zero (a = 0), then on the argand plane it will be located on the imaginary axis either upwards or downwards of the origin depending upon the sign of the imaginary part. That is any point on the imaginary axis will be of the form z = 0 + ib.

Amplitude of any complex number is the angle made by the complex number on the argand plane from the positive real axis.
 

How do you graph a Complex Number?

Let us take few examples to understand that, How can we locate any point on Complex or Argand Plane?

Example 1

Consider a complex number z = 6 +j4 (‘i’ and ‘j’, both can be used for representing imaginary part), if we compare this number with z = a + jb form. Then we can easily equate the two and get a = 6 and b = 4. Since both a and b are positive, which means number will be lying in the first quadrant. ‘z’ will be 6 units in the right and 4 units upwards from the  origin. You can see the same point in the figure below.

Example 2

Now consider a point in the second quadrant i.e. z = -7 + j6, Here since a= -7 and b = 6 and thus will be lying in the second quadrant.

Point z is 7 units in the left and 6 units upwards from the origin. Refer the figure to understand it pictorially.

Example 3

Now let’s consider a point in the third quadrant as z = -2 – j3. Since in third quadrant both a and b are negative and thus a = -2 and b = -3 in our example. This point will be lying 2 units in the left and 3 units downwards from the origin.

Example 4

Let now take the fourth (of fourth quadrant) and the last case where z = 5 – j6. Here, a = 5 and b = – 6 i.e. a positive and b negative. This point will be lying 5 units in the right and 6 units downwards.

What are the different forms of representation of Complex number?

Complex Number itself has many ways in which it can be expressed. Some of the most commonly used forms are:

• Cartesian or algebraic or rectangular form

• Trigonometric or polar form

• Exponential form

• Vector form

We will discuss trigonometric or polar form in detail in next heading.
 

Explain Polar representation in detail

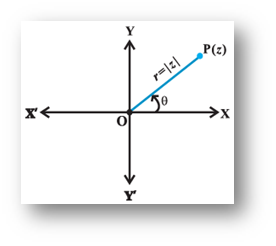
Assume any complex number z = x + iy represented by the point P on the argand plane. O be the origin and OP is the line representing the distance of the Point P from the Origin.

Let, OP or modulus of z is denoted by r. θ be the angle between the line OP and the x - axis or the real axis. Thus, we can say that for any point to be uniquely defined on the argand plane, we need two parameters. Either x (real) and y (imaginary) coordinates or r and θ.

The projection of the point P on the x –axis will be r cos⁡θ, while its projection on y – axis will be r sin ⁡θ.

Thus, we get

x = r cos⁡ θ and y = r sin⁡ θ

So z = x + iy can also be expressed as z = r cos⁡ θ + i r sin⁡ θ.

Or,

z = r(cos⁡θ + isin⁡ θ)

Where,

The above from of the complex number which includes the variables r and θ is called as the Trigonometric or the Polar Form.

Here, r is called as the modulus and θ is its argument or angle.

We also have two other ways of writing complex number in polar form:

• z = r cis θ

• z = r ∠ θ

Arguments itself has three different forms. They are as follows:

• General Argument

• Principle value of argument or amplitude

• Least principle argument

So depending upon the argument, the quadrant may change. Refer the below table to understand it clearly.

Example: Represent z = 1 + j√3 graphically and write it in polar form

Modulus of 

Also, as both its real part and the imaginary parts are positive, so the point will be in first quadrant.

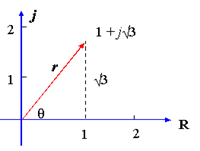Thus, graphically the point will be as:

Graphically, we can easily see that its argument that is 

So, we get r = 2 and θ = 60⁰. 

Thus, z =  1+j√3 = r(cos⁡ θ + i sin⁡ θ) = 2(cos⁡60⁰ + i sin⁡ 60⁰) is its polar form.
 

Is Infinity imaginary number?

Infinity is defined as the inverse of zero. Infinity is not a number neither real number nor any Complex Number. It is just used while expressing the boundaries of real number on the number line that is R ∈ (-∞, ∞). 

Similarly, while expressing the boundaries of real axis and imaginary axis on the argand plane for complex numbers infinity is used.

Although all the algebraic operations can be performed on infinity but, infinity is not considered as any number not even imaginary number.
 

What is a Complex Number plane?

Complex Number plane is another name for the argand plane. This plane is used to represent any complex number graphically. 

Explain Demoivre’s Theorem

Demoivre’s Theorem or DMT (in short) is studied in two cases

Case I: If n ∈ I then

• (cos⁡ θ+ isin θ)ⁿ = cos⁡ nθ + sin ⁡nθ

• (cos⁡θ₁ + i sin⁡θ₁ (cos⁡ θ₂ + i sin⁡ θ₂)………(cos⁡ θn+ i sin⁡ θn) = cos⁡ (θ₁ + θ₂ + …. + θn )+ i sin⁡ ⁡(θ₁ + θ₂ + …. + θ_n)

Case II: If n = p/q, where p, q ∈ Z and q ≠ 0, then

(Cos⁡ θ + i sinθ)^p/q = cos⁡ (2kπ + θ)^p/q + i cos⁡(2nπ + θ) p/q

Where, k = 0, 1, 2, 3, …, (q-1)
 

Application of Demoivre’s Theorem

DMT theorem is mainly used to find the roots of the complex equations.

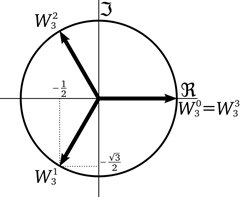
One such application is to find the cube roots of unity.

Assume a cubic equation,

Thus, using DMT theorem, we can re-write it as,

Thus, 1, ω and ω² are called as the cube roots of unity.

This three roots form an equilateral triangle with sides of √3  units of length.

Note:

• ω³ = 1 or ω³ⁿ =1 ∀ n∈I

•  1+ ω+ ω² = 0

This concept can be extended to find the n, n^th roots of unity.

For this, let’s consider n^th degree complex equation having unity root.

Important Note:

•  1, α, α², …, α^n-1 are n, n^th roots of unity which are in G.P. having common ratio, α = e^{i 2π/n}
• 1+ α+ α²+ ……. + α^n-1= 0

Sum of n roots are zero always

Where, case I:  p is not an integral multiple of n

Case II: p is integral multiple ofn and p = nλ, λ∈I

More Readings

Argand Plane and Polar Representation