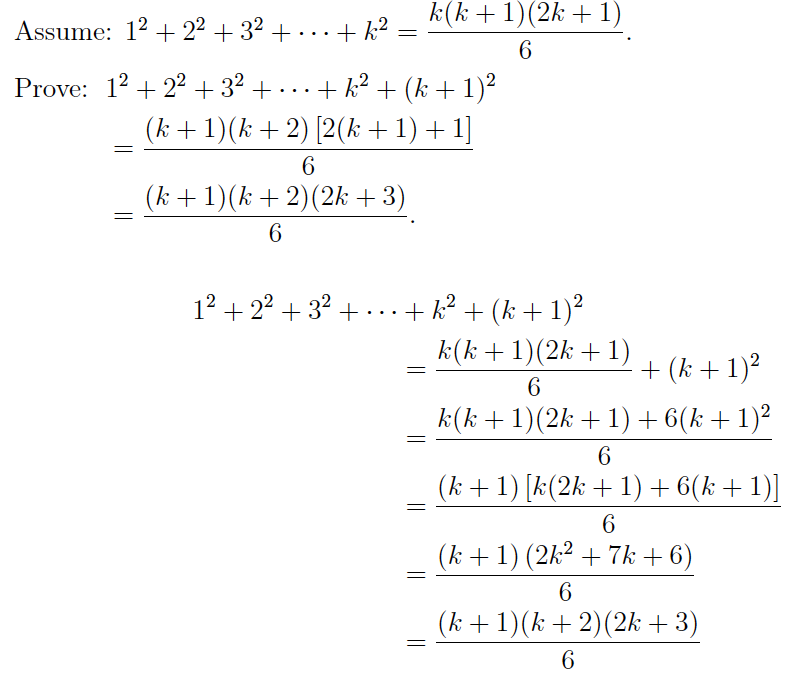Principle of Mathematical Induction

 

Table of Content

History of Mathematical Induction What is Induction in math? Principle of Mathematical Induction First Principle of Mathematical Induction Steps of Mathematical Induction Examples What is Induction Hypothesis? Properties of Principle of Mathematical Induction Second Principle of Mathematical Induction Similarity between First and the Second Principle of Mathematical Induction Difference between First and the Second Principle of Mathematical Induction

What is Induction in math?

Mathematical induction is a special method or technique to prove the statements given in consideration. Generally, it is used to prove the statements of the set of natural numbers.

As in dominoes if we knock the first domino then it shows that the first domino falls, and if we knock any one domino then the next to it will also fall.
 

Principle of Mathematical Induction

Mathematical induction is used to prove that the given statement is true or not. It uses 2 steps to prove it.

First Principle of Mathematical Induction 

• Base Case: The given statement is correct for first natural number that is, for n=1, p (1) is true.

• Inductive Step: If the given statement is true for any natural number like n = k then it will be correct for n = k + 1 also that is, if p (k) is true then p (k+1) will also be true.

The first principle of mathematical induction says that if both the above steps are proven then p (n) is true for all natural numbers.

Second Principle of Mathematical Induction

It is more powerful than the first principle. It is sometimes called as strong induction. It doesn’t need a base case in special case otherwise it may require to show with more than one base case. In the recursive step to prove that k +1 is true, first we need to prove that the statement is correct for all the numbers less than k+1 also.
 

Steps of Mathematical Induction

The mathematical induction can be proved in four steps:

• Given: the statement you want to prove.

• Beginning Step: Show p (1) is true. Let n =1 and solve.

• Assumption Step (Induction Hypothesis): Assume p (k) is true. Let n = k and solve.

• Induction step: Show if p (k) is true then p (k+1) is also true. Let n = k+1 and solve.

Write the proof that p (n) is true.
 

Examples

Example 1

Prove that for any natural number n, the sum of n natural numbers is

 

Solution: Given the statement which we need to prove

Step 1: Base Step

Show the statement holds for n =1

1 = 1(1+1)/2 =2/2 = 1

As the LHS = RHS

This shows that p (1) is true.

Step 2: Inductive Step

Show if p (k) is right then p (k+1) is also right.

Assume p (k) is right

Let n = k

Now we have to prove that it is true for the next number also i.e. k+1

Let n = k+1

Using the induction hypothesis which assumes that p (k) is true, we can rewrite it as:

This shows that p (k+1) is true.

The principle of mathematical induction shows that if both the above steps are true then p (n) is true for all n natural numbers.

Example 2

Prove using mathematical induction that

1² + 2² + 3² + · · · + n² = n (n + 1) (2n + 1)/6 ,for all positive integers n.

Solution: Now we will use base step and induction step to prove it.

Step 1

Let n = 1

The formula is true for n = 1 that is, the statement is true for p (1)

Step 2

Assume p (k) and prove for p (k+1).

Use P(k) to show that P(k + 1) is true.

Therefore, by the Principle of Mathematical Induction,

1² + 2² + 3² + · · · + n² = n (n + 1) (2n + 1) / 6, is true for all positive integers n.

Example 3

Solution:

Step 1

Show p (1) is true.

So p (1) is true.

Step 2

Assume p (k) is true.

Show if p (k) is true then p (k+1) is also true.

Now use p (k) and p (1) to prove it.

This shows that this statement is true for p (k+1) also.

Hence p (n) is true.
 

What is Induction Hypothesis?

In the principle of mathematical induction when we reach to the inductive step, we need to assume p (k) to prove the statement for p (k+1).that assumption is induction hypothesis.

Example

Prove using induction hypothesis: sum of odd natural numbers is n².

Solution: Theorem: 1 + 3 + 5 + 7 +…+ 2n – 1 = n²

  Step 1: Base step

Show the statement holds for n =1

1 = n² = 1

As the LHS = RHS
 

Properties of Principle of Mathematical Induction

• Base Step is basically a statement of fact which shows that the statement is true for the first number of the set of natural numbers. If it is given that the statement is true for n ≥ 3, then we will start with n = 3 and verify that for n = 3, p (3) is true.

• Inductive Step is the conditional property of mathematical induction. As it is not the statement which state that n = k, but it is the condition that if statement is true for n = k then it will be true for n = k + 1 also.
   

Second Principle of Mathematical Induction

If we want to prove that every positive integer can be factored into prime.

Let M is a subset of the set of all natural numbers.

1, 2, . . . , l ∈ M and l ∈ N, and

for any k ≥ l, we have 1, 2, . . . , k ∈ M implies k + 1 ∈ M.

Then M = N.

We will show it in terms of group of propositions.

Let P₁, P₂, P₃, . . . be a group of propositions. Suppose 

• Base Case

For some l ∈ N,

P₁, P₂, . . . , P_l

are all correct, and

• Recursive Step

For any k ≥ l, if P₁, P₂, . . . , P_k are all correct, then P _k+1 is also correct;

Then P_n is true for all n ∈ N.

This shows that, to prove P _k+1, we can assume not only that P_k is true, but that all previous P_j are also true.

In this principle we do not need to start at n = 1.

We can use more than one base case, to prove this step.

As we know that a prime number is any positive number which is greater than 1 and which has no factors other than itself and 1.

Some prime numbers are:

2, 5, 11, 17, 19, 23, 29, 31.

Now we will factorize a positive integer into prime factors. For Example:

105 = 3 × 5 × 7.

Example

Prove that every natural number that is, n > 1 is either prime or a product of prime numbers using the second principle of induction.

Solution:

For each n ≥ 2, let P_n is the set of numbers that either:

• n is prime, or

•  n is a product of primes,

n = p₁p₂ · · · p_r, all p_i prime.

We shall prove P₂, P₃, . . . are all true.

In this case we only need one base case and we will start at n = 2

Base Case:  2 is a prime number, so P₂ is true.

Recursive Step: Suppose k ≥ 2 is such that P₂, P₃, . . . , P_k are all true.

Hence all the numbers of 2, 3, . . . , k is either prime or a product of primes.

Now we will show P _k+1 is true: that is, k + 1 is prime or a product of primes.

There are two options: either k + 1 is prime or not.

• If k + 1 is prime, then P _k+1 is true.

• If k + 1 is not prime, then by definition there exists integers p, q for which k + 1 = pq, where 1 < p, q < k + 1.

But by the induction hypothesis, both Pp and Pq are true.

So we can write

p = p₁p₂ · · · p_r,

q = q₁q₂ · · · q_s,

where p₁, p₂, . . . , p_r, q₁, q₂, . . . , q_s are primes.

So

k + 1 = pq = p₁p₂ · · · p_rq₁q₂ · · · q_s,

which is a product of primes. So P _k+1 is true.

So whether or not k + 1 is prime, P _k+1 is true.

Hence by the second principle of induction, Pn is true for all n ≥ 2.
 

Similarity between First and the Second Principle of Mathematical Induction

Both the method of induction gives the same result so that both the inductions are equivalent. It doesn’t mean that strong induction gives the better result than the ordinary induction.

As both the induction gives the same result, the proof of one method can be converted into another and vice versa.

Suppose we have a proof of P (n) by strong induction. Let R (n) mean "P (m) holds for all m such that 0 ≤ m ≤ n". Then R (n) is correct for all n if and only if P (n) is true for all n, and our proof of P (n) is easily converted into a proof of R (n) by weak induction. If, on the other hand, P(n) had been proven by weak induction, the proof would already be one by strong induction: In the base case P(0) is proved, without using assumptions, and in the inductive step P(n + 1) is proved, in which one may assume all earlier cases but need only use the P(n) case.
 

Difference between First and the Second Principle of Mathematical Induction

	First Principle of Mathematical Induction	Second Principle of Mathematical Induction
1.	It is also known as weak induction or ordinary induction.	It is also known as strong induction or complete induction.
2.	It is difficult form of induction.	It is the easiest form of induction.
3.	In base case, one has to show for p(1)	In base case ,one has to show for p(0) and sometimes some extra base case also like p(1) etc.
4.	In inductive step, it assumes p (n).	In recursive step, one proves the statement P (n + 1), under the assumption that P (n) is true for all natural numbers less than n + 1.

Watch this Video for more reference
 

More Readings

Principle of Mathematical Induction