Linear Simple Harmonic Oscillator

The block − spring system is a linear simple harmonic oscillator. All oscillating systems like diving board, violin string have some element of springiness, k (spring constant) and some element of inertia, m.

Horizontal oscillations of spring

Consider a mass (m) attached to an end of a spiral spring (which obeys Hooke’s law) whose other end is fixed to a support as shown in figure. The body is placed on a smooth horizontal surface. Let the body be displaced through a distance x towards right and released. It will oscillate about its mean position. The restoring force acts in the opposite direction and is proportional to the displacement.

So, Restoring force F = −kx.

From Newton’s second law, we know that, F = ma.

ma  = −kx

a = (– k/m) x

Comparing with the equation of SHM a = – ω²x, we get,

 ω² = k/m

Or, ω = √k/m

But T = 2π/ω

Time period, T = 2π√m/k

Thus, frequency, n = 1/T = (1/2π)√k/m

Therefore,

Vertical oscillations of a spring

Figure shows a light, elastic spiral spring suspended vertically from a rigid support in a relaxed position. When a mass ‘m’ is attached to the spring as in figure, the spring is extended by a small length dl such that the upward force F exerted by the spring is equal to the weight mg.

The restoring force               F = k dl ;              k dl = mg                       ...(1)

where k is spring constant. If we further extend the given spring by a small distance by applying a small force by our finger, the spring oscillates up and down about its mean position. Now suppose the body is at a distance y above the equilibrium position as in figure. The extension of the spring is (dl − y). The upward force exerted on the body is k (dl − y) and the resultant force F on the body is,

F = k (dl − y) − mg = −ky                   …... (2)

The resultant force is proportional to the displacement of the body from its equilibrium position and the motion is simple harmonic.

If the total extension produced is (dl + y) as in figure the restoring force on the body is k (dl + y) which acts upwards.

So, the increase in the upward force on the spring is k (dl + y) −mg = ky

Therefore if we produce an extension downward then the restoring force in the spring increases by ky in the upward direction. As the force acts in the opposite direction to that of displacement, the restoring force is − ky and the motion is SHM.

F = -ky

ma = – ky

a = (– k/m) y           …... (3)

a = – ω²y        (expression for SHM)

Comparing the above equations, ω = √k/m              …... (4)

But, T = 2π/ω = 2π√m/k            …... (5)

From equation (1), mg = kdl

m/k = dl/g

Therefore time period, T = 2π√dl/g         …... (6)

Frequency, n = (1/2π) √g/dl

Case 1 : When two springs are connected in parallel

Two springs of spring factors k₁ and k₂ are suspended from a rigid support as shown in figure. A load m is attached to the combination.

Let the load be pulled downwards through a distance y from its equilibrium position. The increase in length is y for both the springs but their restoring forces are different.

If F₁ and F₂ are the restoring forces

F₁ = −k₁y,               F₂ = −k₂y

∴ Total restoring force = (F₁ + F₂) = −(k₁ + k₂₎ y

So, time period of the body is given by,

T = 2π√m/k₁+k₂

If k₁ = k₂ = k

Then, T = 2π√(m/2k)  

So, frequency, n = (1/2π)√(2k/m)

Thus,

Case 2 : When two springs are connected in series.

Two springs are connected in series in two different ways. This arrangement is shown in Fig. 6.12a and 6.12b.

In this system when the combination of two springs is displaced to a distance y, it produces extension y₁ and y₂ in two springs of force constants k₁ and k₂.

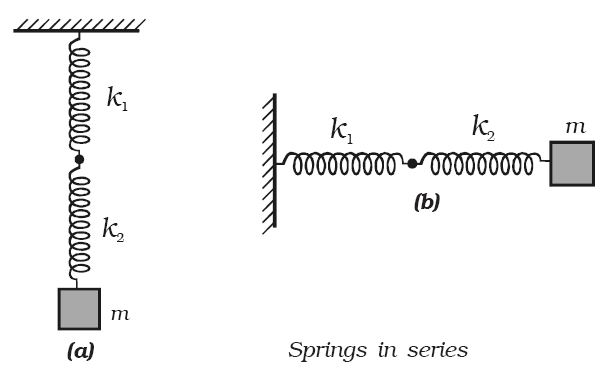
  F = – k₁y₁   and F = – k₂y₂

Where F is the restoring force.

Total extension, y = y₁ + y₂ = – F [1/k₁ + 1/k₂]

We know that, F = -ky

So, y = – F/k

From the above equation,

– F/k = – F [1/k₁ + 1/k₂]

Or, k = k₁k₂/k₁ + k₂

Thus, time period = T = 2π√[m(k₁ + k₂)/k₁k₂]

frequency, n = (1/2π) √[k₁k₂/m(k₁ + k₂)]

If both the springs have the same spring constant,

k₁ = k₂ = k

So, n = 1/2π √k/2m

Thus,

Refer this video to know more about, “Energy of Simple Harmonic Oscillator”.

Oscillation of liquid column in a U - tube

Consider a non viscous liquid column of length l of uniform cross-sectional area A (Fig. 6.13). Initially the level of liquid in the limbs is the same. If the liquid on one side of the tube is depressed by blowing gently the levels of the liquid oscillates for a short time about their initial positions O and C, before coming to rest.

If the liquid in one of the limbs is depressed by y , there will be a difference of 2 y in the liquid levels in the two limbs. At some instant, suppose the level of the liquid on the left side of the tube is at D, at a height y above its original position O, the level B of the liquid on the other side is then at a depth y below its original position C. So the excess pressure P on the liquid due to the restoring force is excess height × density × g

(i.e) pressure = 2 y ρ g

∴ Force on the liquid = pressure × area of the cross-section of the tube

= – 2 y ρ g × A                …... (1)

The negative sign indicates that the force towards O is opposite to the displacement measured from O at that instant.

The mass of the liquid column of length l is volume × density

(i.e)  m = l A ρ

∴ F = l A ρ a              …... (2)

From equations (1) and (2)   l A ρ a = - 2 y A ρ g

So, a = – (2g/l) y        …... (3)

We know that, a = – ω²y

So, a = – (2g/l) y = – ω²y

Here, ω = √2g/l

Here, the acceleration is proportional to the displacement, so the motion is simple harmonic and the period T is,

T = 2π/ω = 2π√l/2g

So,

Problem (JEE Main):

A block of mass 15 kg executes SHM under the restoring force of a spring. The amplitude and the time period of the motion are 0.1 m and 3.14 s respectively. Find the maximum force exerted by the spring on the block.

Data : m = 15 kg, a = 0.1 m and T = 3.14 s

Solution:

Solution : The maximum force exerted on the block is ka, when the block is at the extreme position, where k is the spring constant.

The angular frequency = ω = 2π/T = 2s^-1

The spring constant k = mω² = 154 = 60 Nm^-1

The maximum force exerted on the block is ka = 600.1 = 6 N

Question 1

Which of the following is the necessary condition for SHM?

(a) constant period 

(b) constant acceleration 

(c) displacement and acceleration are proportional

(d) displacement and torque are proportional 

Question 2

A linear harmonic oscillator has a total energy of 160 J. Its

(a) maximum potential energy is 100 J

(b) maximum kinetic energy is 160 J

(c) minimum potential energy is 100 J

(d) maximum kinetic energy is 100 J 

Question 3

The displacement of a particle executing SHM is given by x = 0.01 sin (100 πt + 0.05). Its time period is,

(a) 0.01 s          (b) 0.02 s

(c) 0.1 s            (d) 0.2 s

Question 4

If the magnitude of displacement is equal to acceleration, then the time period is,

(a) 1 s                (b) π s

(c) 2π s               (d) 4π s

Question 5

A particle executes SHM along a straight line with an amplitude ‘a’ ⋅PE is maximum when the displacement is

(a) ± a                 (b) zero

(c) +a/2                (d) a/√2

Related Resources:-

• You might like to simple harmonic motion. 

• For getting an idea of the type of questions asked, refer the  Previous Year Question Papers.

• Click here to refer the most Useful Books of Physics.

• To get answer to any question related to linear simple harmonic oscillator click here.