Chapter 14: Coordinate Geometry Exercise – 14.3

Question: 1

Find the coordinates of the point which divides the line segment joining (-1, 3) and (4, - 7) internally in the ratio 3 : 4.

Solution:

Let P(x, y) be the required point.

Here, x₁ = - 1

y₁ = 3

x₂  = 4

y₂ = -7

m : n = 3 : 4

∴ The coordinates of P are (8/7, – 9/7)

 

Question: 2

Find the points of trisection of the line segment joining the points:

(i) (5, - 6) and (-7, 5)

(ii) (3, - 2) and (-3, - 4)

(iii) (2, - 2) and (-7, 4)

Solution:

(i) Let P and Q be the point of trisection of AB i.e., AP = PQ = QB

Therefore. P divides AB internally in the ratio of 1: 2, thereby applying section formula, the coordinates of P will be

Now, Q also divides AB internally in the ratio of 2:1 there its coordinates are

 (ii) Let P, Q be the point of tri section of AB i.e. ,

AP = PQ = QB

Therefore, P divides AB internally in the ratio of 1: 2. Hence by applying section formula. Coordinates of P are

Now, Q also divides as internally in the ratio of 2: 1

So, the coordinates of Q are

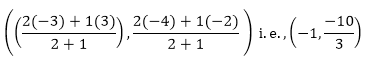
Let P and Q be the points of trisection of AB i.e., AP = PQ = OQ

Therefore, P divides AB internally in the ratio 1:2. Therefore, the coordinates of P, by applying the section formula, are

Now. Q also divides AB internally in the ration 2 : 1. So the coordinates of Q are

 

Question: 3

Find the coordinates of the point where the diagonals of the parallelogram formed by joining the points (-2, -1), (1, 0), (4, 3) and (1, 2) meet.

Solution:

Let P(x, y) be the given points.

We know that diagonals of a parallelogram bisect each other.

∴  coordinates of P are (1, 1)

 

Question: 4

Prove that the points (3, 2), (4, 0), (6, -3) and (5, -5) are the vertices of a parallelogram.

Solution:

Let P(x, y) be the point of intersection of diagonals AC and 80 of ABCD.

Again,

Here mid-point of AC — Mid - point of BD i.e. diagonals AC and BD bisect each other.

We know that diagonals of a parallelogram bisect each other

∴ ABCD is a parallelogram.

 

Question: 5

Three consecutive vertices of a parallelogram are (- 2, -1), (1, 0) and (4, 3). Find the fourth vertex.

Solution:

Let A (-2,—1), B (1, 0), C (4, 3)and D (x, y) be the vertices of a parallelogram ABCD taken in order.

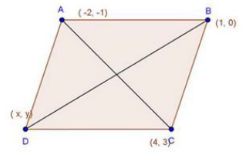Since the diagonals of a parallelogram bisect each other.

∴ Coordinates of the mid - point of AC = Coordinates of the mid-point of BD.

⇒ x + 1 = 2

⇒ x = 1

And,

Hence, fourth vertex of the parallelogram is (1, 2)