Chapter 13: Linear Equation in Two Variables Exercise – 13.3
Question: 1
Draw the graph of each of the following linear equations in two variables:
(i) x + y = 4
(ii) x - y = 2
(iii) -x + y = 6
(iv) y = 2x
(v) 3x + 5y = 15

(viii) 2y = -x +1
Solution:
(i) We are given, x + y = 4
We get, y = 4 - x,
Now, substituting x = 0 in y = 4 - x,
We get y = 4
Substituting x = 4 in y = 4 - x, we get y = 0
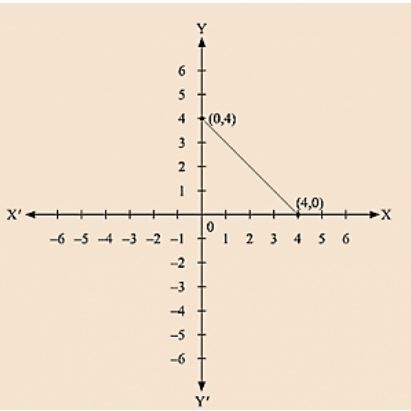
Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given table
| X | 0 | 4 |
| Y | 4 | 0 |
(ii) We are given, x - y = 2
We get, y = x – 2
Now, substituting x = 0 in y= x – 2, we get y = - 2
Substituting x = 2 in y = x – 2, we get y = 0
Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation
| X | 0 | 2 |
| Y | - 2 | 0 |

(iii) We are given, - x + y = 6
We get, y = 6 + x
Now, substituting x = 0 in y = 6 + x,
We get y = 6
Substituting x = - 6 in y = 6 + x, we get y = 0
Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation.
| X | 0 | - 6 |
| Y | 6 | 0 |

(iv) We are given, y = 2x
Now, substituting x = 1 in y = 2x, we get y = 2
Substituting x = 3 in y = 2x, we get y = 6
Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation
| X | 1 | 3 |
| Y | 2 | 6 |

(v) We are given, 3x + 5y = 15
We get, 15 - 3x = 5y
Now, substituting x = 0 in 5y = 15 - 3x,
We get; 5y = 15 y = 3
Substituting x = 5 in 5y = 15 – 3x we get 5y = 0
Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation
| X | 0 | 5 |
| Y | 3 | 0 |

(vi) we are given.

3x - 2y = 12
We get,

We get y = - 6
Substituting x = 4 in

We get y = 0 Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation
| X | 0 | 4 |
| Y | - 6 | 0 |

(vii) We are given,

We get, x - 2 = 3(y - 3)
x - 2 = 3y - 9
x = 3y - 7
Now, substituting x = 5 in x = 3y - 7,
We get; y = 4
Substituting x = 8 in x = 3y - 7,
We get; y = 5
Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation
| X | 5 | 8 |
| Y | 4 | 5 |

(viii) We are given, 2y = - x +1
We get, 1 – x = 2y
Now, substituting x = 1 in 1– x = 2y, we get y = 0
Substituting x = 5 in 1 – x = 2y, we get y = - 2
Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation
| X | 1 | 5 |
| Y | 0 | - 2 |

Question: 2
Give the equations of two lines passing through (3, 12). How many more such lines are there, and why?
Solution:
We observe that x = 3 and y = 12 is the solution of the following equations 4x – y = 0 and 3x – y + 3 = 0
So, we get the equations of two lines passing through (3, 12) are, 4x - y = 0 and 3x - y + 3 = 0.
We know that passing through the given point infinitely many lines can be drawn. So, there are infinitely many lines passing through (3, 12)
Question: 3
A three-wheeler scooter charges Rs 15 for first kilometer and Rs 8 each for every subsequent kilometer. For a distance of x km, an amount of Rs y is paid. Write the linear equation representing the above information.
Solution:
Total fare of Rs y for covering the distance of x km is given by y = 15 + 8(x - 1)
y = 15 + 8x - 8
y = 8x + 7
Where, Rs y is the total fare (x - 1) is taken as the cost of first kilometer is already given Rs 15 and 1 has to subtracted from the total distance travelled to deduct the cost of first Kilometer.
Question: 4
A lending library has a fixed charge for the first three days and an additional charge for each day thereafter. Aarushi paid Rs 27 for a book kept for seven days. If fixed charges are Rs x and per day charges are Rs y. Write the linear equation representing the above information.
Solution:
Total charges of Rs 27 of which Rs x for first three days and Rs y per day for 4 more days is given by x + y (7 – 3) = 27
x + 4y = 27
Here, (7 - 3) is taken as the charges for the first three days are already given at Rs x and we have to find the charges for the remaining four days as the book is kept for the total of 7 days.
Question: 5
A number is 27 more than the number obtained by reversing its digits. lf its unit's and ten's digit are x and y respectively, write the linear equation representing the statement.
Solution:
The number given to us is in the form of ‘yx‘,
Where y represents the ten's place of the number And x represents the unit's place of the number.
Now, the given number is 10y + x
Number obtained by reversing the digits of the number is 10x + y It is given to us that the original number is 27 more than the number obtained by reversing its digits So, 10y + x = 10x + y + 27
10y – y + x - 10x = 27
9y - 9x = 27
9(y – x) = 27
y – x = 27/9
3x – y + 3 = 0
Question: 6
The Sum of a two digit number and the number obtained by reversing the order of its digits is 121. If units and tens digit of the number are x and y respectively, then write the linear equation representing the above statement.
Solution:
The number given to us is in the form of ‘yx’,
Where y represents the ten's place of the number and x represents the units place of the number
Now, the given number is 10y + x
Number obtained by reversing the digits of the number is 10x+ y
It is given to us that the sum of these two numbers is 121 So, (10y + x) + (10x + y) = 121
10y + y + x + 10x = 121
11y + 11x = 121
11(y + x) = 121
x + y = 121/11 = 11
x + y = 11
Question: 7
Plot the Points (3, 5) and (-1, 3) on a graph paper and verify that the straight line passing through the points, also passes through the point (1, 4)
Solution:

By plotting the given points (3, 5) and (-1, 3) on a graph paper, we get the line BC.
We have already plotted the point A (1, 4) on the given plane by the intersecting lines.
Therefore, it is proved that the straight line passing through (3, 5) and (-1, 3) also passes through A (1, 4).
Question: 8
From the choices given below, choose the equations whose graph is given in fig
(i) y = x
(ii) x + y = 0
(iii) y = 2x
(iv) 2 + 3y = 7x
Solution:
We are given co-ordinates (1, - 1) and (-1, 1) as the solution of one of the following equations.
We will substitute the value of both co-ordinates in each of the equation and find the equation which satisfies the given co-ordinates.
 (i) We are given, y = x
(i) We are given, y = x
Substituting x =I and y = - 1, we get; 1 ≠ -1
L.H.S ≠ R.H.S
Substituting x = -1 and y = 1, we get; – 1 ≠1
L.H.S ≠ R.H.S
Therefore, the given equation y = x does not represent the graph in the figure.
(ii) We are given, x + y = 0
Substituting x = 1 and y = -1, we get
⟹ 1 + (-1) = 0
⟹ 0 = 0
L.H.S = R.H.S
Substituting x = 1 and y = 1, we get (-1) + 1 = 0
0 = 0
L.H.S = R.H.S
Therefore, the given solutions satisfy this equation.
Thus, it is the equation whose graph is given.
Question: 9
From the choices given below, choose the equation whose graph is given fig:
(i) y = x + 2
(ii) y = x – 2
(iii) y = - x + 2
(iv) x + 2y = 6
Solution:
We are given co-ordinates (-1, 3) and (2, 0) as the solution of one of the following equations.
We will substitute the value of both co-ordinates in each of the equation and find the equation which satisfies the given co-ordinates.
(i) We are given, y=x+2 Substituting x = - 1 and y = 3,
 We get 3 ≠ -1+ 2
We get 3 ≠ -1+ 2
L.H.S ≠ R.H.S
Substituting x = 2 and y = 0,
We get 0 ≠ 4
L.H.S ≠ R.H.S
Therefore, the given solution does not satisfy this equation.
(ii) We are given, y = x - 2
Substituting x = 1 and y = 3,
We get 3 = - 1 - 2
L.H.S ≠ R.H.S
Substituting x = 2 and y = 0, we get 0 = 0
L.H.S = R.H.S
Therefore, the given solutions does not completely satisfy this equation.
(iii) We are given, y = - x + 2
Substituting x = - 1 and y = 3,
We get 3 = - (-1) + 2
L.H.S = R.H.S
Substituting x = 2 and y = 0, we get 0 = - 2 + 2
0 = 0
L.H.S = R.H.S
Therefore, the given solutions satisfy this equation. Thus, it is the equation whose graph is given.
Question: 10
If the point (2, -2) lies on the graph of linear equation, 5x + 4y = 4, find the value of k.
Solution:
It is given that the point (2,-2) lies on the given equation, 5x + ky = 4
Clearly, the given point is the solution of the given equation.
Now, Substituting x = 2 and y = - 2 in the given equation, we get 5x + ky = 4
5 × 2 + (- 2) k = 4
2k = 10 – 4
2k = 6
k = 6/2
k = 3
Question: 11
Draw the graph of equation 2x + 3y = 12.
From the graph, find the co-ordinates of the point:
(i) whose y-coordinate is 3
(ii) whose x coordinate is -3
Solution:
We are given, 2x + 3y = 12
We get,

Substituting, x = 0 in

We get,

y = 4
Substituting x = 6 in

y = 12 – 2 × 63
y = 0
Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation
| X | 0 | 6 |
| Y | 4 | 0 |

By plotting the given equation on the graph, we get the point B(0, 4) and C (6,0).
(i) Co-ordinates of the point whose y axis is 3 are A (3/2, 3)
(ii) Co-ordinates of the point whose x -coordinate is -3 are D (- 3, 6)
Question: 12
Draw the graph of each of the equations given below. Also, find the coordinates of the points where the graph cuts the coordinate axes:
(i) 6x – 3y = 12
(ii) - x + 4y = 8
(iii) 2x + y = 6
(iv) 3x + 2y + 6 = 0
Solution:
(i) We are given, 6x - 3y = 12
We get, y = (6x -12)/3
Now, substituting x = 0 in y = - (6x – 12)/3
we get y = - 4
Substituting x = 2 in y = (- 6x -12)/3, we get y = 0
Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation
| X | 0 | 2 |
| Y | - 4 | 0 |

Co-ordinates of the points where graph cuts the co-ordinate axes are y = - 4 at y axis and x = 2 at x axis.
(ii) We are given, - x + 4y = 8
We get,

Now, substituting x = 0 in

we get y = 2
Substituting x = - 8 in

We get y = 0
Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation
| X | 0 | - 8 |
| Y | 2 | 0 |

Co-ordinates of the points where graph cuts the co-ordinate axes are y = 2 at y axis and x = -8 at x axis.
(iii) We are given, 2x + y = 6
We get, y = 6 - 2x
Now, substituting x = 0 in y = 6 - 2x we get y = 6
Substituting x = 3 in y = 6 - 2x, we get y = 0
Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation
| X | 0 | 3 |
| Y | 6 | 0 |

Co-ordinates of the points where graph cuts the co-ordinate axes are y = 6 at y axis and x = 3 at x axis.
(iv) We are given, 3x + 2y + 6 = 0
We get,

Now, substituting x = 0 in

Substituting x = 2 in

we get y = 0
Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation
| X | 0 | - 2 |
| Y | - 3 | 0 |

Co-ordinates of the points where graph cuts the co-ordinate axes are y = - 3 at y axis and x = - 2 at x axis.
Question: 13
Draw the graph of the equation 2x + y = 6. Shade the region bounded by the graph and the coordinate axes. Also, find the area of the shaded region.
Solution:
We are given, 2x + y = 6
We get, y = 6 - 2x
Now, substituting x = 0 in y = 6 - 2x,
we get y = 6
Substituting x = 3 in y = 6 - 2x, we get y = 0
Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation
| X | 0 | 3 |
| Y | 6 | 0 |

The region bounded by the graph is ABC which forms a triangle.
AC at y axis is the base of triangle having AC = 6 units on y axis.
BC at x axis is the height of triangle having BC = 3 units on x axis.
Therefore, Area of triangle ABC, say A is given by A = (Base x Height)/2
A = (AC × BC)/2
A = (6 × 3)/2
A = 9 sq. units
Question: 14
Draw the graph of the equation x/3 + y/4 = 1. Also, find the area of the triangle formed by 3/4 the line and the coordinates axes.
Solution:
We are given. x/3 + y/4 = 1
4x + 3y =12

Now, substituting x = 0 in

we get y = 4
Substituting x = 3 in

we get y = 0
Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation
| X | 0 | 3 |
| Y | 4 | 0 |

The region bounded by the graph is ABC which forms a triangle.
AC at y axis is the base of triangle having AC = 4 units on y axis.
BC at x axis is the height of triangle having BC = 3 units on x axis.
Therefore, Area of triangle ABC, say A is given by A = (Base × Height)/2
A= (AC × BC)/2
A = (4 × 3)/2
A = 6 sq. units
Question: 15
Draw the graph of y = |×|.
Solution:
We are given, y = |x|
Substituting x = 1, we get y = 1
Substituting x = - 1, we get y = 1
Substituting x = 2, we get y = 2
Substituting x = - 2, we get y = 2

For every value of x, whether positive or negative, we get y as a positive number.
Question: 16
Draw the graph of y = |x| + 2.
Solution:
We are given, y = |x| + 2
Substituting x = 0 we get y = 2
Substituting x = 1, we get y = 3
Substituting x = - 1, we get y = 3
Substituting x = 2, we get y = 4
Substituting x = - 2, we get y = 4

For every value of x, whether positive or negative, we get y as a positive number and the minimum value of y is equal to 2 units.
Question: 17
Draw the graphs of the following linear equations on the same graph paper: 2x + 3y = 12, x - y = 1 Find the coordinates of the vertices of the triangle formed by the two straight lines and the y-axis. Also, find the area of the triangle.
Solution:
We are given, 2x +3y =12
We get,

Now, substituting x = 0 in

we get y = 4
Substituting x = 6 in

we get y = 0
Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation
| X | 0 | 6 |
| Y | 4 | 0 |
Plotting A (0, 4) and E(6, 0) on the graph and by joining the points ,
we obtain the graph of equation 2x + 3y = 12.
We are given, x – y = 1
We get, y = x – 1
Now, substituting x = 0 in y = x - 1, we get y = -1
Substituting x in y = x - 1, we get y = -2
Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation
| X | 0 | -1 |
| Y | -1 | -2 |
Plotting D (0, – 1) and E (-1, 0) on the graph and by joining the points, we obtain the graph of equation x - y = 1.

By the intersection of lines formed by 2x + 3y = 12 and x - y = 1 on the graph, triangle ABC is formed on y axis.
Therefore, AC at y axis is the base of triangle ABC having AC = 5 units on y axis.
Draw FE perpendicular from F on y axis.
FE parallel to x axis is the height of triangle ABC having FE = 3 units on x axis.
Therefore, Area of triangle ABC, say A is given by A = (Base × Height)/2 = (AC × FE)/2 = (5× 3)/2 =>15/2 = 7.5 sq. units
Question: 18
Draw the graphs of the linear equations 4x - 3y + 4 = 0 and 4x + 3y - 20 = 0. Find the area bounded by these lines and x-axis.
Solution:
We are given, 4x - 3y + 4 = 0
We get,

Now, substituting x = 0 in

we get
Substituting x = -1 in

we get y = 0
Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation
| x | 0 | -1 |
| y | 3/4 | 0 |
Plotting E(0, 4/3) and A (-1, 0) on the graph and by joining the points,
We obtain the graph of equation 4x - 3y + 4 = 0.
We are given, 4x + 3y - 20 = 0
We get,

Now, substituting x = 0 in

we get y = 7
Substituting x = 5 in

we get y = 0
Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation
| X | 0 | 5 |
| Y | 20/3 | 0 |
Plotting D (0, 20/3) and B (5, 0) on the graph and by joining the points, we obtain the graph of equation 4x +3y - 20 = 0.

By the intersection of lines formed by 4x - 3y + 4 = 0 and 4x + 3y - 20 = 0 on the graph,
Triangle ABC is formed on x axis.
Therefore, AB at x axis is the base of triangle ABC having AB = 6 units on x axis.
Draw CF perpendicular from C on x axis. CF parallel to y axis is the height of triangle ABC having CF = 4 units on y axis.
Therefore, Area of triangle ABC, say A is given by A = (Base × Height)/2
A = (AB × CF)/2
A = (6 × 4)/2
K = 12 sq. units
Question: 19
The path of a train A is given by the equation 3x + 4y -12 = 0 and the path of another train B is given by the equation 6x + 8y - 48 = 0. Represent this situation graphically.
Solution:
We are given the path of train A, 3x + 4y - 12 = 0
We get,

Now, substituting x = 0 in

we get y = 3
Substituting x = 4 in

we get y = 0
Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation
| X | 0 | 4 |
| Y | 3 | 0 |
Plotting A(4, 0) and E(0, 3) on the graph and by joining the points,
we obtain the graph of equation 3x + 4y - 12 = 0.
We are given the path of train B, 6x + 8y - 48 = 0
We get,

Now, substituting x = 0 in

we get y = 6
Substituting x = 8 in

we get y = 0
Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation
| X | 0 | 8 |
| Y | 6 | 0 |
Plotting C (0, 6) and D (8, 0) on the graph and by joining the points. We obtain the graph of equation 6x + 8y – 48 = 0

Question: 20
Ravish tells his daughter Aarushi, "Seven years ago, I was seven times as old as you were then. Also, three years from now, I shall be three times as old as you will be". If present ages of Aarushi and Ravish are x and y years respectively, represent this situation algebraically as well as graphically.
Solution:
We are given the present age of Ravish as y years and Aarushi as x years.
Age of Ravish seven years ago = y - 7
Age of Aarushi seven years ago = x – 7
It has already been said by Ravish that seven years ago he was seven times old then Aarushi was then So, y - 7 = 7( x – 7)
y – 7 = 7x – 49
7x - y = - 7 + 49
7x – y – 42 = 0 .... (1)
Age of Ravish three years from now = y + 3
Age of Aarushi three years from now = x + 3
It has already been said by Ravish that three years from now he will be three times older then Aarushi will be then So, Y + 3 = 3 (x + 3)
y + 3 = 3x + 9
3x + 9 – y – 3 = 0
3x – y + 6 = 0 ..... (2)
(1) and (2) are the algebraic representation of the given statement.
We are given, 7x - y- 42 = 0
We get, y = 7x – 42
Now, substituting x = 0 in y = 7x – 42, we get y = – 42
Substituting x = 6 in y = 7x - 42, we get y = 0
Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation
| X | 0 | 6 |
| Y | - 42 | 0 |
We are given, 3x – y + 6 = 0
We get, Y = 3x + 6
Now, substituting x = 0 in y = 3x + 6, We get y = 6
Substituting x = -2 in y = 3x + 6,
We get y = 0
Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation
| X | 0 | -2 |
| Y | 6 | 0 |

The red – line represents the equation 7x - y - 42 = 0.
The blue-line represents the equation 3x - y + 6 = 0.
Question: 21
Aarushi was driving a car with uniform speed of 60 km/h. Draw distance-time graph From the graph, find the distance travelled by Aarushi in
(i) 5/2 Hours
(ii) 1/2 Hour
Solution:
Aarushi is driving the car with the uniform speed of 60 km/h. We represent time on X-axis and distance on Y-axis Now, graphically

We are given that the car is travelling with a uniform speed 60 km/hr.
This means car travels 60 km distance each hour.
Thus the graph we get is of a straight line.
Also, we know when the car is at rest, the distance travelled is 0 km, speed is 0 km/hr and the time is also 0 hr.
Thus, the given straight line will pass through O(0, 0) and M(1, 60).
Join the points 0 and M and extend the line in both directions.
Now, we draw a dotted line parallel to y-axis from x = 12 that meets the straight line graph at L from which we draw a line parallel to x-axis that crosses y-axis at 30.
Thus, in 12 hr, distance travelled by the car is 30 km.
Now, we draw a dotted line parallel to y-axis from x = 5/2 that meets the straight line graph at N from which we draw a line parallel to x-axis that crosses y-axis at 150.
Thus, in 5/2 hr, distance travelled by the car is 150 km.
(i) Distance = Speed × Time Distance travelled in 5/2 hours is given by
Distance = 60 × 5/2, Distance = 150 Km
(ii) Distance = Speed × Time Distance travelled in 12 hour is given by Distance = 60 × 5/2
Distance = 30 km