Revision Notes on Chemical Kinetics:

Rate of Reaction:

Rate of change of extent of reaction is the rate of reaction.
Rate of reaction is positive for product and negative for reactant.
For reaction aA →bB
Rate =1/b(Δ[B]/ Δ t) = -1/a (Δ [A]/ Δt)
It goes on decreasing as the reaction progress due to decrease in the concentration(s) of the reactant(s).

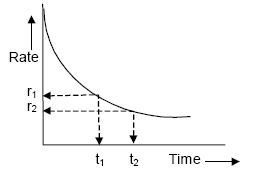
Unit of rate of reaction : mol L^-1s^-1
The rate measured over a long time interval is called average rate and the rate measured for an infinitesimally small time interval is called instantaneous rate.
In a chemical change, reactants and products are involved. As the chemical reaction proceeds, the concentration of the reactants decreases, i.e., products are produced.
The rate of reaction (average rate) is defined as the change of concentration of any one of its reactants (or products) per unit time.

Order of Reaction

For reaction aA + bB + ….. → cC+ ….

R ∝[A]^m[B]ⁿor R = k[A]^m[B]ⁿ….

Where m and n may or may not be equal to a & b.

m is order of reaction with respect to A and n is the order of reaction with respect to B.

m + n +… is the overall order of the reaction.

Elementary Reaction:

It is the reaction which completes in a single step.
A reaction may involve more than one elementary reactions or steps also.
Overall rate of reaction depends on the slowest elementary step and thus it is known as rate determining step.

Molecularity of Reaction:

Number of molecules taking part in an elementary step is known as its molecularity.
Order of an elementary reaction is always equal to its molecularity.
Elementary reactions with molecularity greater than three are not known because collisions in which more than three particles come together simultaneously are rare.

Chemical Reaction	Molecularity
PCl₅ → PCl₃ + Cl₂	Unimolecular
2HI → H₂ + I₂	Bimolecular
2SO₂ + O₂ → 2SO₃	Trimolecular
NO + O₃ → NO₂ + O₂	Bimolecular
2CO + O₂ → 2CO₂	Trimolecular
2FeCl₃ + SnCl₂ → SnCl₂ + 2FeCl₂	Trimolecular

Differential and Integrated Rate Laws:

Zero Order Reactions:

Characteristic of Zero Order Reaction

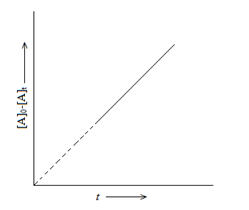
For Reaction: A → Product

[A]₀-[A]_t = k₀t

Where,

[A]_{0 =}Initial concentration of A

[A]_t= Concentration of A at time t.

k₀= Rate constant for zero order reaction.

Half Life:

t_1/2 = [A]₀/2k

Unit of rate constant = mol dm^-3s^-1

Examples:

Enzyme catalyzed reactions are zero order with respect to substrate concentration.
Decomposition of gases on the surface of metallic catalysts like decomposition of HI on gold surface.

First Order Reactions:

Characteristic of First Order Reaction

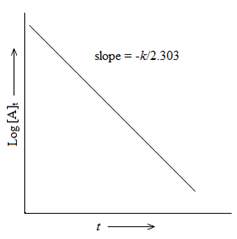
A → Product

(Δ [A] /A) = -k₁Δt

or k₁=( 2.303/ t)log ([A]₀/ [A]_t)

Half Life:

t_1/2 = 0.693/k₁

Half life is independent of the initial concentration of the reactant for a first order reaction.

Units of k₁ = s^-¹

Examples:

N₂O₅→ 2NO₂ + 1/2O₂

Br₂ → 2Br

2HNO₃ → 2NO + H₂O

H₂O₂→ H₂O + 1/2O₂

Pseudo First Order Reactions:

These are the reactions in which more than one species is involved in the rate determining step but still the order of reaction is one.

Examples:

Acid hydrolysis of ester: CH₃COOEt + H₃O⁺ →CH₃COOH + EtOH
Inversion of cane sugar:

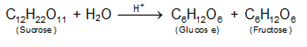
Decomposition of benzenediazonium halides C₆H₅N=NCl +H₂O → C₆H₅OH +N₂ +HCl

Half – Life of a nth Order Reaction:

kt_1/2 = (2^n-1-1)/(n-1)[A₀]^n-1

Where, n = order of reaction ≠1

Parallel Reactions:

The reactions in which a substance reacts or decomposes in more than one way are called parallel or side reactions.

reaction-in-which-a-decomposes

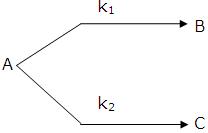
If we assume that both of them are first order, we get.

$-\frac{d[A]}{dt} = (k_1 +k_2) [A] =k_{av}[A]$

k₁ = fractional yield of B × k_av

k₂ = fractional yield of C × k_av

If k₁ > k₂ then

A → B main and

A → C is side reaction

Let after a definite interval x mol/litre of B and y mol/litre of C are formed.

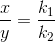
$\frac{x}{y} =\frac{k_1}{k_2}$

i.e

$\frac{\frac{d[B]}{dt}}{\frac{d[C]}{dt}} =\frac{k_1}{k_2}$

This means that irrespective of how much time is elapsed, the ratio of concentration of B to that of C from the start (assuming no B and C in the beginning ) is a constant equal to k₁/k₂.

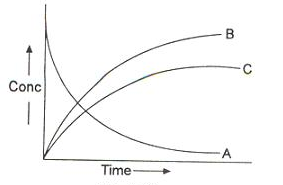
pLOT FOR Parallel or Competing Reaction

Parallel and Sequential Reactions

Sequential Reactions:

This reaction is defined as that reaction which proceeds from reactants to final products through one or more intermediate stages. The overall reaction is a result of several successive or consecutive steps.

A → B → C and so on

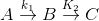
$A\overset{k_1}{\rightarrow}B\overset{K_2}{\rightarrow}C$

$-\frac{d[A]}{dt} = k_1[A]$ …....(i)

$\frac{d[B]}{dt} = k_1[A]-K_2[B]$ …......(ii)

$\frac{d[C]}{dt} = k_2[B]$ ….......(iii)

Integrating equation (i), we get

$[A]-[A]_oe^{-k_1t}$

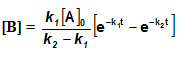
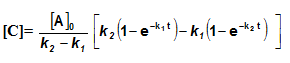
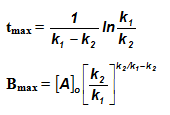
Arrhenius Equation:

k = A exp(-E_a/RT)

Where, k = Rate constant

A = pre-exponential factor

E_a = Activation energy

Temperature Coefficient:

The temperature coefficient of a chemical reaction is defined as the ratio of the specific reaction rates of a reaction at two temperature differing by 10^oC.

μ = Temperature coefficient= k_(r+10)/k_t

Let temperature coefficient of a reaction be ' μ ' when temperature is raised from T₁to T₂; then the ratio of rate constants or rate may be calculated as

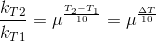
$\frac{k_T_2}{k_T_1}=\mu ^\frac{{T_2-T_1}}{10} =\mu ^{\frac{\Delta T}{10}}$

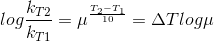
$log\frac{k_T_2}{k_T_1}=\mu ^\frac{{T_2-T_1}}{10} =\Delta T log\mu$

$\frac{k_T_2}{k_T_1}= antilog[\frac{\Delta T}{10 }] log\mu$

Its value lies generally between 2 and 3.

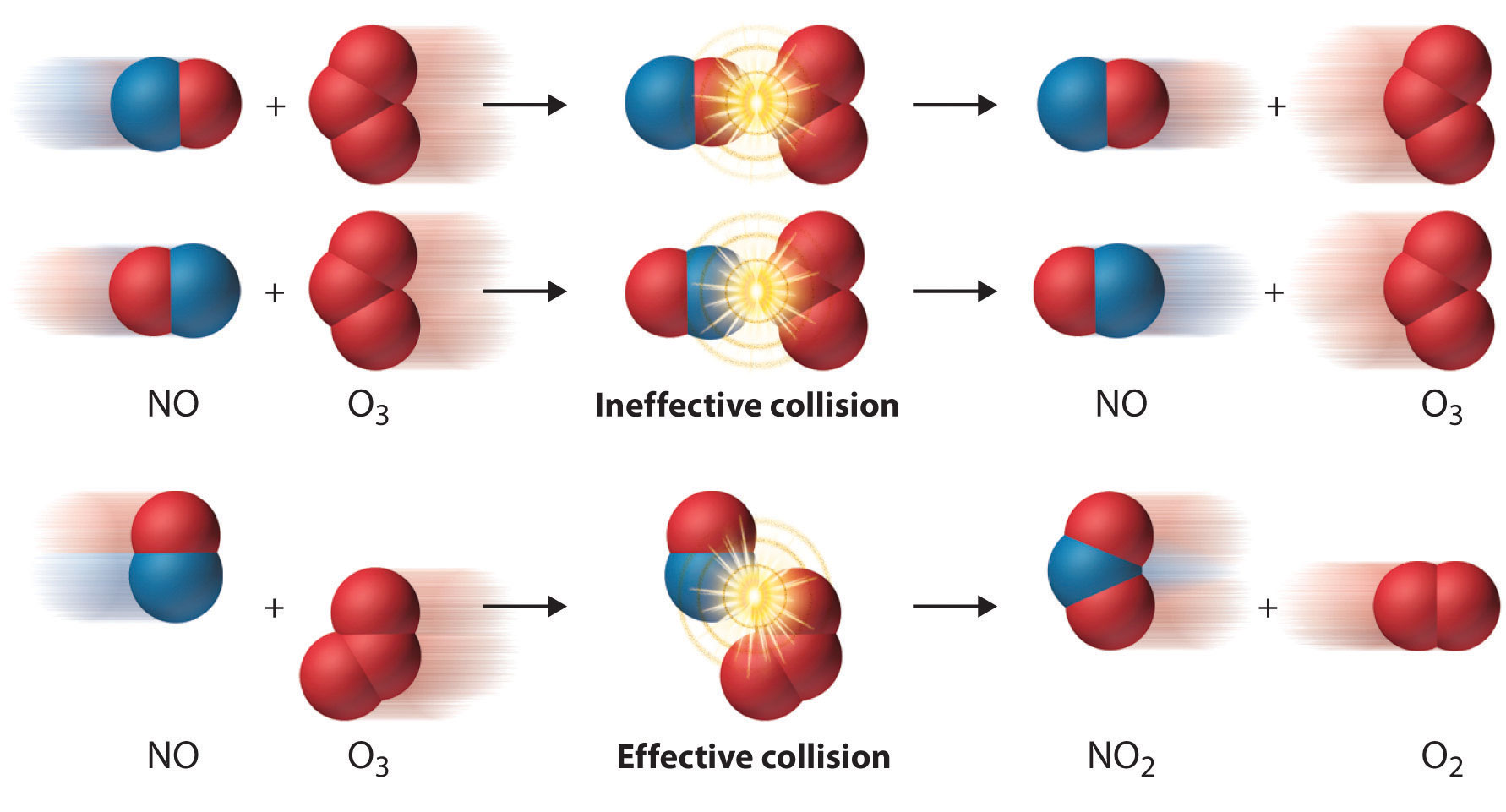
Collision Theory of Reaction Rate

A chemical reaction takes place due to collision among reactant molecules.
The number of collisions taking place per second per unit volume of the reaction mixture is known as collision frequency (Z).
The value of collision frequency is very high, of the order of 10²⁵ to 10²⁸ in case of binary collisions.
Every collision does not bring a chemical change.
The collisions that actually produce the products are effective collisions.
The effective collisions which bring chemical change are few in comparison to the form a product are ineffective elastic collisions, i.e., molecules just collide and
disperse in different directions with different velocities.
For a collision to be effective, the following two barriers are to be cleared.

Energy Barrier
Orientation Barrier

Radioactivity:

All radioactive decay follow 1^st order kinetics

For radioactive decay A ->B

-(dN_A/dt) =l N_A

Where, l = decay constant of reaction

N_A = number of nuclei of the radioactive substance at the time when rate is calculated.

Arrhenius equation is not valid for radioactive decay.

Integrated Rate Law: N_t= N_oe^-^l^t

Half Life: t_1/2= 0.693/λ

Average life time: Life time of a single isolated nucleus, t_av= 1/λ

Activity: Rate of decay

A = dN_A/dt, Also, A_t= A_oe^-^l^t

Specific Activity: activity per unit mass of the sample.

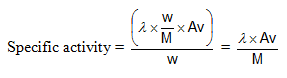
Units: dps or Becquerrel

Live courses Ask question