Rational numbers (Class 8th) - Revision Notes
Rational Numbers
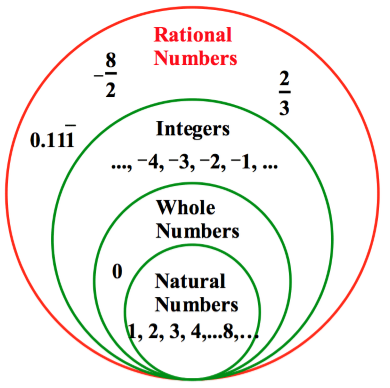
A number is called Rational if it can be expressed in the form p/q where p and q are integers (q > 0). It includes all natural, whole number and integers.
Example: 1/2, 4/3, 5/7,1 etc.
Natural Numbers
All the positive integers from 1, 2, 3,……, ∞.
Whole Numbers
All the natural numbers including zero are called Whole Numbers.
Integers
All negative and positive numbers including zero are called Integers.
Properties of Rational Numbers
1. Closure Property
This shows that the operation of any two same types of numbers is also the same type or not.
a. Whole Numbers
If p and q are two whole numbers then
| Operation | Addition | Subtraction | Multiplication | Division |
|
Whole number |
p + q will also be the whole number. |
p – q will not always be a whole number. |
pq will also be the whole number. |
p ÷ q will not always be a whole number. |
|
Example |
6 + 0 = 6 |
8 – 10 = – 2 |
3 × 5 = 15 |
3 ÷ 5 = 3/5 |
|
Closed or Not |
Closed |
Not closed |
Closed |
Not closed |
b. Integers
If p and q are two integers then
| Operation | Addition | Subtraction | Multiplication | Division |
|
Integers |
p+q will also be an integer. |
p-q will also be an integer. |
pq will also be an integer. |
p ÷ q will not always be an integer. |
|
Example |
- 3 + 2 = – 1 |
5 – 7 = – 2 |
- 5 × 8 = – 40 |
- 5 ÷ 7 = – 5/7 |
|
Closed or not |
Closed |
Closed |
Closed |
Not closed |
c. Rational Numbers
If p and q are two rational numbers then
| Operation | Addition | Subtraction | Multiplication | Division |
|
Rational Numbers |
p + q will also be a rational number. |
p – q will also be a rational number. |
pq will also be a rational number. |
p ÷ q will not always be a rational number |
|
Example |
|
|
|
p ÷ 0 = not defined |
|
Closed or Not |
Closed |
Closed |
Closed |
Not closed |
2. Commutative Property
This shows that the position of numbers does not matter i.e. if you swap the positions of the numbers then also the result will be the same.
a. Whole Numbers
If p and q are two whole numbers then
| Operation | Addition | Subtraction | Multiplication | Division |
|
Whole number |
p + q = q + p |
p – q ≠ q – p |
p × q = q × p |
p ÷ q ≠ q ÷ p |
|
Example |
3 + 2 = 2 + 3 |
8 –10 ≠ 10 – 8 – 2 ≠ 2 |
3 × 5 = 5 × 3 |
3 ÷ 5 ≠ 5 ÷ 3 |
|
Commutative |
yes |
No |
yes |
No |
b. Integers
If p and q are two integers then
| Operation | Addition | Subtraction | Multiplication | Division |
|
Integers |
p + q = q + p |
p – q ≠ q – p |
p × q = q × p |
p ÷ q ≠ q ÷ p |
|
Example |
True |
5 – 7 = – 7 – (5) |
- 5 × 8 = 8 × (–5) |
- 5 ÷ 7 ≠ 7 ÷ (-5) |
|
Commutative |
yes |
No |
yes |
No |
c. Rational Numbers
If p and q are two rational numbers then
| Operation | Addition | Subtraction | Multiplication | Division |
|
Rational numbers |
p + q = q + p |
p –q ≠ q - p |
p × q = q × p |
p ÷ q ≠ q ÷ p |
|
Example |
|
|
|
|
|
Commutative |
yes |
No |
yes |
No |
3. Associative Property
This shows that the grouping of numbers does not matter i.e. we can use operations on any two numbers first and the result will be the same.
a. Whole Numbers
If p, q and r are three whole numbers then
| Operation | Addition | Subtraction | Multiplication | Division |
|
Whole number |
p + (q + r) = (p + q) + r |
p – (q – r) = (p – q) – r |
p × (q × r) = (p × q) × r |
p ÷ (q ÷ r) ≠ (p ÷ q) ÷ r |
|
Example |
3 + (2 + 5) = (3 + 2) + 5 |
8 – (10 – 2) ≠ (8 -10) – 2 |
3 × (5 × 2) = (3 × 5) × 2 |
10 ÷ (5 ÷ 1) ≠ (10 ÷ 5) ÷ 1 |
|
Associative |
yes |
No |
yes |
No |
b. Integers
If p, q and r are three integers then
| Operation | Integers | Example | Associative |
|
Addition |
p + (q + r) = (p + q) + r |
(– 6) + [(– 4)+(–5)] = [(– 6) +(– 4)] + (–5) |
Yes |
|
Subtraction |
p – (q – r) = (p – q) – r |
5 – (7 – 3) ≠ (5 – 7) – 3 |
No |
|
Multiplication |
p × (q × r) = (p × q) × r |
(– 4) × [(– 8) ×(–5)] = [(– 4) × (– 8)] × (–5) |
Yes |
|
Division |
p ÷ (q ÷ r) ≠ (p ÷ q) ÷ r |
[(–10) ÷ 2] ÷ (–5) ≠ (–10) ÷ [2 ÷ (– 5)] |
No |
c. Rational Numbers
If p, q and r are three rational numbers then
| Operation | Integers | Example | Associative |
|
Addition |
p + (q + r) = (p + q) + r |
|
yes |
|
Subtraction |
p – (q – r) = (p – q) – r |
|
No |
|
Multiplication |
p × (q × r) = (p × q) × r |
|
yes |
|
Division |
p ÷ (q ÷ r) ≠ (p ÷ q) ÷ r |
|
No |
The Role of Zero in Numbers (Additive Identity)
Zero is the additive identity for whole numbers, integers and rational numbers.
| Identity | Example | ||
|
Whole number |
a + 0 = 0 + a = a |
Addition of zero to whole number |
2 + 0 = 0 + 2 = 2 |
|
Integer |
b + 0 = 0 + b = b |
Addition of zero to an integer |
False |
|
Rational number |
c + 0 = 0 + c = c |
Addition of zero to a rational number |
2/5 + 0 = 0 + 2/5 = 2/5 |
The Role of one in Numbers (Multiplicative Identity)
One is the multiplicative identity for whole numbers, integers and rational numbers.
| Identity | Example | ||
|
Whole number |
a ×1 = a |
Multiplication of one to the whole number |
5 × 1 = 5 |
|
Integer |
b × 1= b |
Multiplication of one to an integer |
- 5 × 1 = – 5 |
|
Rational Number |
c × 1= c |
Multiplication of one to a rational number |
 |
Negative of a Number (Additive Inverse)
| Identity | Example | ||
|
Whole number |
a +(- a) = 0 |
Where a is a whole number |
5 + (-5) = 0 |
|
Integer |
b +(- b) = 0 |
Where b is an integer |
True |
|
Rational number |
c + (-c) = 0 |
Where c is a rational number |
 |
Reciprocal (Multiplicative Inverse)
The multiplicative inverse of any rational number
Example
The reciprocal of 4/5 is 5/4.
Distributivity of Multiplication over Addition and Subtraction for Rational Numbers
This shows that for all rational numbers p, q and r
1. p(q + r) = pq + pr
2. p(q – r) = pq – pr
Example
Check the distributive property of the three rational numbers 4/7,-( 2)/3 and 1/2.
Solution
Let’s find the value of
This shows that
Representation of Rational Numbers on the Number Line
On the number line, we can represent the Natural numbers, whole numbers and integers as follows
Rational Numbers can be represented as follows
Rational Numbers between Two Rational Numbers
There could be n number of rational numbers between two rational numbers. There are two methods to find rational numbers between two rational numbers.
Method 1
We have to find the equivalent fraction of the given rational numbers and write the rational numbers which come in between these numbers. These numbers are the required rational numbers.
Example
Find the rational number between 1/10 and 2/10.
Solution
As we can see that there are no visible rational numbers between these two numbers. So we need to write the equivalent fraction.
2/10 = 20/100((multiply the numerator and denominator by 10)
Hence, 2/100, 3/100, 4/100……19/100 are all the rational numbers between 1/10 and 2/10.
Method 2
We have to find the mean (average) of the two given rational numbers and the mean is the required rational number.
Example
Find the rational number between 1/10 and 2/10.
Solution
To find mean we have to divide the sum of two rational numbers by 2.
3/20 is the required rational numbers and we can find more by continuing the same process with the old and the new rational number.
Remark: 1. This shows that if p and q are two rational numbers then (p + q)/2 is a rational number between p and q so that
p < (p + q)/2 < q.
2. There are infinite rational numbers between any two rational numbers.