Revision Notes on Alternating Current

• Alternating Current:-

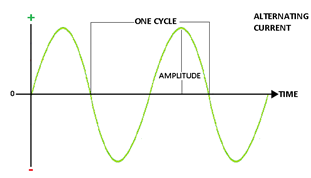An alternating current (a.c.) is a current which continuously, changes in magnitude and periodically reverses in direction.`

i = I₀ sin ωt = I₀ sin (2π/T) t

Here I₀ is the peak value of a.c.

(a) Current, I =I₀ sin ωt

(b) Angular frequency, ω= 2πn   (n is the frequency of a.c.)

(c) I =I₀ sin 2πnt

• Mean value of A.C or D.C. value of A.C.:-

Mean value of a.c. is that value of steady current which sends the same amount of charge, through a circuit, in same time as is done by a.c. in one half-cycle.

(I_av)_{half cycle} = (2/π)I₀

Thus, mean value of alternating current is 2/π times (0.637 times) its peak value.

(V_av)_{half cycle} = (2/π) V₀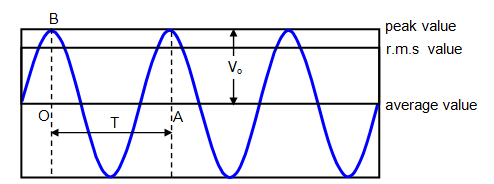

• Average value of A.C. over a complete cycle:-

I_av = 0

The average value of a.c. taken over the complete cycle of a.c.is zero.

• Root mean square value of a.c. or virtual value of a.c.:-

Root mean square value of alternating current is defined as that value of steady current which produces same heating effect, in a resistance, in a certain time as is produced by the alternating current in same resistance in same time. The r.m.s value of a.c.is also called its virtual value.

I_rms = I₀/√2

Root mean square value of alternating current is I/√2 times (or 0.707 times) the peak value of current.

Similarly, V_rms= V₀/√2

Here V₀ is the peak value of e.m.f.

• Form Factor:-

Form Factor = rms value/average value = (V₀/√2)/ (2 V₀/π)  = π/2√2

• Current elements:-

(a) Inductive reactance:- X_L = ωL

Here, ω = 2πn, n being frequency of a.c.

L is the coefficient of self-inductance of coil.

(b) Capacitative reactance:- X_c = 1/ωC

Here C is the capacity of the condenser

• Capacitor in AC circuit:-

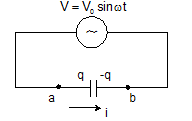q = CV₀sinωt

I = I₀ sin(ωt +π/2)

V₀ = I₀/ωC

X_c = 1/ωC

• Inductor in AC circuit:-

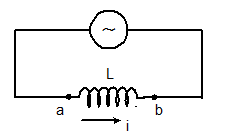V_L = L(dI/dt) = LI₀ω cosωt

I = (V₀/ ωL) sinωt

Here, I₀ = V₀/ ωL

X_L = ωL

And the maximum current, I₀ = V₀/XL

• R-L circuit:-

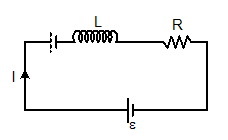I = ε/R [1-e^-Rt/L]

V = ε e^-Rt/L

• Graph between I (amp) and t (sec):-

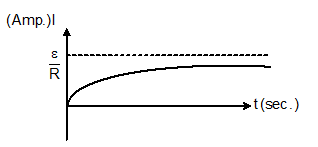
• Graph between potential difference across inductor and time:-

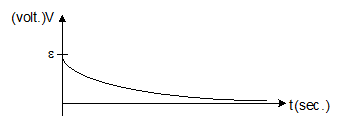
• L-C Circuit:-

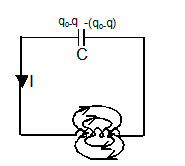f = 1/2π√LC

q = q₀ sin (ωt+ϕ)

I = q₀ωsin (ωt+ϕ)

ω = 1/√LC

• The total energy of the system remains conserved,

  ½ CV² + ½ Li² = constant = ½ CV₀² = ½ Li₀²

• Series in C-R circuit:-

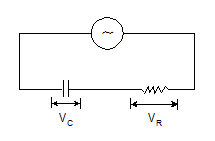
 V = IZ

The modulus of impedance, |Z |= √R²+(1/ωC)²

The potential difference lags the current by an angle, ϕ = tan^-1(1/ωCR)

• Series in L-C-R Circuit:

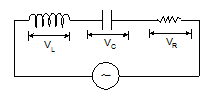
V = IZ

The modulus of impedance, |Z |= √[R²+(ωL-1/ωC)²]

The potential difference lags the current by an angle, ϕ = tan^-1[ωL -1/ωC)/R]

• Circuit elements with A.C:-

Circuit elements	Amplitude relation	Circuit quantity	Phase of V
Resistor	V0 = i0R	R	In phase with i
Capacitor	V0 = i0XC	C	Lags i by 90°
Inductor	V0 = i0XL	XL = wL	Leads i by 90°

• Resonance:-

(a) Resonance frequency:- f_r = 1/2π√LC

(b) At resonance, X_L = X_C, ϕ = 0, Z = R(minimum), cosϕ = 1, sinϕ = 0 nad current is maximum (=E₀/R)

• Half power frequencies:-

(a) Lower,  f₁ = f_r – R/4πL    or      ω₁ = ω_r – R/2L

(b) Upper,  f₂ = f_r + R/4πL    or      ω₂ = ω_r + R/2L

• Band width:- Δf = R/2πL   or   Δf = R/L

• Quality Factor:-

(a) Q = ω_r/Δω = ω_rL/R

(b) As ω = 1/√LC, So Q ∝ √L, Q ∝1/R and Q ∝ 1/√C

(c) Q = 1/ω_rCR

(d) Q = X_L/R   or  Q = X_C/R 

(e) Q = f_r/Δf   

• At resonance, peak voltages are:-

(a) (V_L)_res = e₀Q

(b) (V_C)_res = e₀Q

(c) (V_R)_res = e₀

• Conductance, susceptance and admittance:-

(a) Conductance, G = 1/R

(b) Susceptance, S = 1/X

(c) S_L = 1/X_L and S_C = 1/X_C = ωC

(d) Admittance, Y = 1/Z

(e) Impedance add in series while add in parallel

• Power in AC circuits:-

Circuit containing pure resistance:- P_av = (E₀/√2)×(I₀/√2) = E_v×I_v

Here E_v and I_v are the virtual values of e.m.f and the current respectively.

Circuit containing impedance (a combination of R,L and C):-

P_av = (E₀/√2)×(I₀/√2) cosϕ = (E_v×I_v) cosϕ

Here cosϕ is the power factor.

(a) Circuit containing pure resistance, P_av = E_vI_v

(b) Circuit containing pure inductance, P_av = 0

(c) Circuit containing pure capacitance, P_av = 0

(d) Circuit containing resistance and inductance,

Z = √R²+(ωL)

cosϕ = R/Z = R/[√{R²+(ωL)²}]

(e) Circuit containing resistance and capacitance:-

Z = √R²+(1/ωC)²

cosϕ = R/Z = R/[√{R²+(1/ωC)²}]

(f) Power factor, cosϕ = Real power/Virtual power = P_av/E_rmsI_rms

• Transformer:-

(a) C_p = N_p (dϕ/dt) and e_s = N_s (dϕ/dt)

(b) e_p/e_s = N_p/N_s

(c) As, e_pI_p = e_sI_s, Thus, I_s/I_p = e_p/e_s = N_p/N_s

(d) Step down:- e_s < e_p, N_s< N_p and I_s> I_p

(e) Step up:- e_s >e_p, N_s>N_p and I_s< I_p

(f) Efficiency, η = e_s I_s/ e_p I_p

• AC Generator:-

e = e₀ sin (2πft)

Here, e₀ = NBAω