Revision Notes on Gravitation and Projectile

Gravitation:-

• Kepler’s first law (law of elliptical orbit):- A planet moves round the sun in an elliptical orbit with sun situated at one of its foci.

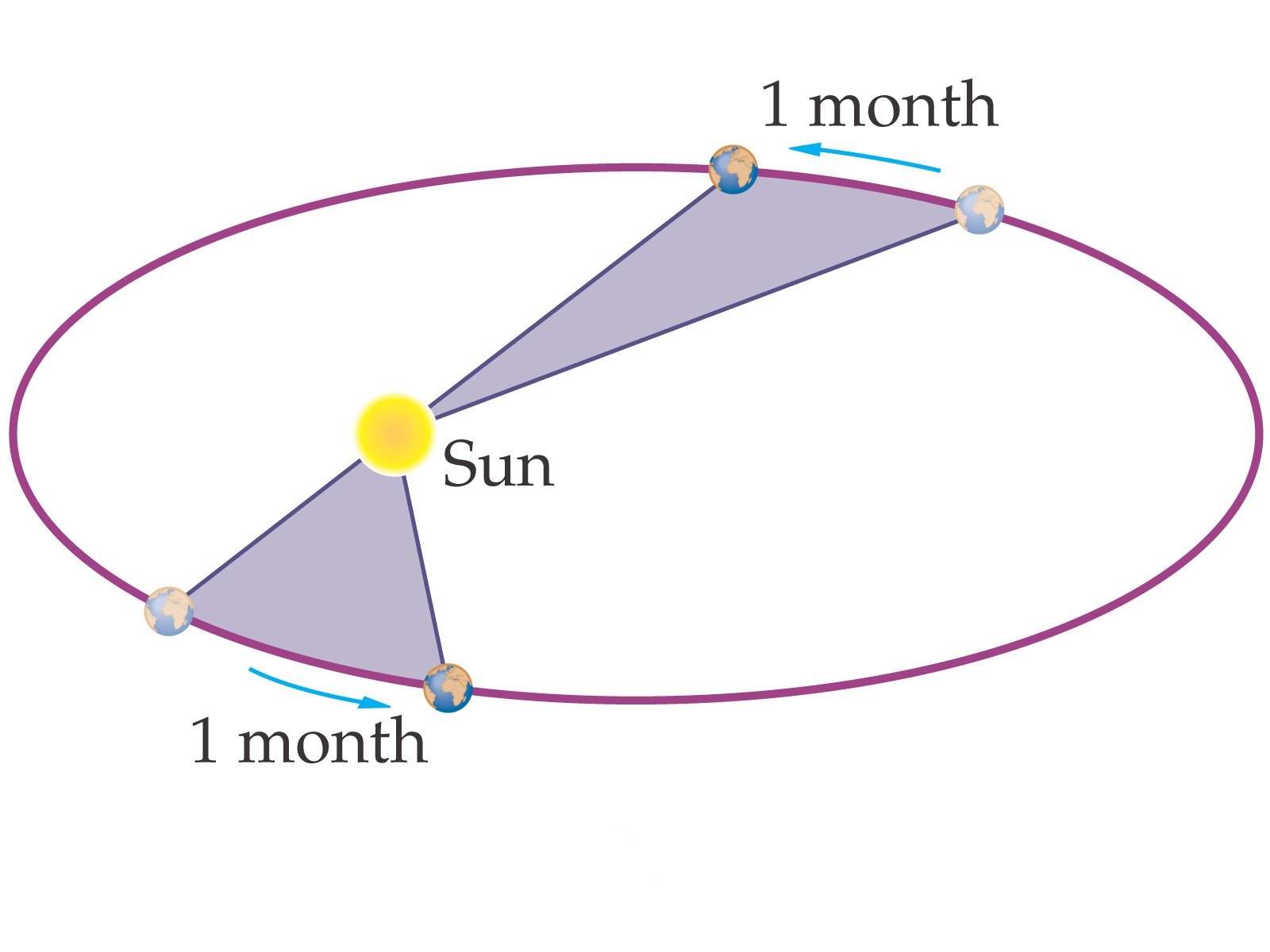
• Kepler’s second law (law of areal velocities):- A planet moves round the sun in such a way that its areal velocity is constant.

• Kepler’s third law (law of time period):- A planet moves round the sun in such a way that the square of its period is proportional to the cube of semi major axis of its elliptical orbit.

T² ∝ R³

Here R is the radius of orbit.

T² = (4π²/GM)R ³

• Newton’s law of gravitation:-

Every particle of matter in this universe attracts every other particle with a forcer which varies directly as the product of masses of two particles and inversely as the square of the distance between them.

F= GMm/r²

Here, G is universal gravitational constant. G = 6.67 ´10 ^-11 Nm² / kg²

• Dimensional formula of G: G = Fr²/Mm =[MLT^-2][L²]/[M²] = [M^-1L³T^-2]

• Acceleration due to gravity (g):- g = GM/R²

• Variation of g with altitude:- g' = g(1- 2h/R),  if h<<R. Here R is the radius of earth and h is the height of the body above the surface of earth.

• Variation of g with depth:- g' = g(1- d/R). Here g' be the value of acceleration due to gravity at the depth d.

• Variation with latitude:-

At poles:- θ = 90^°, g^' = g

At equator:- θ = 0^°, g^' = g (1-ω²R/g)

Here ω is the angular velocity.

• As g = GM_e/R_e² , therefore g_pole > g_equator

• Gravitational Mass:- m = FR²/GM

• Gravitational field intensity:-

E = F/m

= GM/r²

• Weight:- W= mg

• Gravitational intensity on the surface of earth (E_s):-

E_s = 4/3 (πRρG)

Here R is the radius of earth, ρ is the density of earth and G is the gravitational constant.

• Gravitational potential energy (U):- U = -GMm/r

(a) Two particles: U = -Gm₁m₂/r

(b) hree particles: U = -Gm₁m₂/r₁₂ – Gm₁m₃/r₁₃ – Gm₂m₃/r₂₃

• Gravitational potential (V):- V(r) =  -GM/r

At surface of earth,

V_s=  -GM/R

Here R is the radius of earth.

• Escape velocity (v_e):-

It is defined as the least velocity with which a body must be projected vertically upward   in order that it may just escape the gravitational pull of earth.

v_e = √2GM/R

or, v_e = √2gR = √gD

Here R is the radius of earth and D is the diameter of the earth.

• Escape velocity (v_e) in terms of earth’s density:- v_e = R√8πGρ/3

• Orbital velocity (v₀):-

v₀ = √GM/r

If a satellite  of mass m revolves in a circular orbit around the earth of radius R and h be the height of the satellite above the surface of the earth, then,

r = R+h

So, v₀ = √MG/R+h = R√g/R+h

In the case of satellite, orbiting very close to the surface of earth, then orbital velocity will be,

v₀ = √gR

• Relation between escape velocity ve and orbital velocity v₀ :- v₀= v_e/√2  (if h<<R)

• Time period of Satellite:- Time period of a satellite is the time taken by the satellite to complete one revolution around the earth.

T = 2π√(R+h)³/GM = (2π/R)√(R+h)³/g

If h<<R, T = 2π√R/g

• Height of satellite:- h = [gR²T²/4π²]1/3 – R

• Energy of satellite:-

Kinetic energy, K = ½ mv₀² = ½ (GMm/r)

Potential energy, U = - GMm/r

Total energy, E = K+U

= ½ (GMm/r) + (- GMm/r)

= -½ (GMm/r)

• Gravitational force in terms of potential energy:- F = – (dU/dR)

• Acceleration on moon:-

g_m = GM_m/R_m² = 1/6 g_earth 

Here M_m is the mass of moon and R_m is the radius of moon.

• Gravitational field:-

(a)    Inside:-

 

(b)   Outside:-

 

• GRAVITATIONAL POTENTIAL & FIELD DUE TO VARIOUS OBJECTS

Causing Shape	Gravitational Potential (V)	Gravitational Field (I or E)	Graph V vs R
POINT MASS
AT A POINT ON THE AXIS OF RING
ROD
1. AT AN AXIAL POINT
	V = –
2. AT AN EQUATORIAL POINT
CIRCULAR ARC
HOLLOW SPHERE
SOLID SPHERE
LONG THREAD
	V = ∞

Projectile:-

• Projectile fired at angle α  with the horizontal:- If a particle having initial speed u is projected at an angle α (angle of projection) with x-axis, then,

Time of Ascent, t = (u sinα)/g

Total time of Flight, T = (2u sinα)/g

Horizontal Range, R = u²sin2α/g

Maximum Height, H = u²sin²α/2g

Equation of trajectory, y = xtanα-(gx²/2u²cos²α)

Instantaneous velocity, V=√(u²+g²t²-2ugt sinα)

and         

β = tan^-1(usinα-gt/ucosα)

• Projectile fired horizontally from a certain height:-

Equation of trajectory: x² = (2u²/g)y

Time of descent (timer taken by the projectile to come down to the surface of earth), T = √2h/g

Horizontal Range, H = u√2h/g. Here u is the initial velocity of the body in horizontal direction.

Instantaneous velocity:-

V=√u²+g²t²

If β be the angle which V makes with the horizontal, then,

β = tan^-1(-gt/u)

• Projectile fired at angle α with the vertical:-

Time of Ascent, t = (u cosα)/g

Total time of Flight, T = (2u cosα)/g

Horizontal Range, R = u²sin2α/g

Maximum Height, H = u²cos²α/2g

Equation of trajectory, y = x cotα-(gx²/2u²sin²α)

Instantaneous velocity, V=√(u²+g²t²-2ugt cosα) and β = tan^-1(ucosα-gt/usinα)

• Projectile fired from the base of an inclined plane:-

Horizontal Range, R = 2u² cos(α+β) sinβ/gcos²α

Time of flight, T = 2u sinβ/ gcosα

Here, α+β=θ

 

You Might Like to Refer:

CBSE class 8 physics | CBSE class 8 chemistry | CBSE class 10 physics