Propositions on Ellipse
Table of Content |
The standard equation of an ellipse referred to its principal axes along the coordiante axes is x2/a2 + y2/b2 =1, where
a > b and b2 = a2(1-e2), where e = eccentricity lies between 0 and 1, i.e. 0 < e < 1.
It has two focii S(ae, 0),and S’(-ae, 0).
Position of a point with respect to Ellipse
The point P(x1, y1) lies outside, inside or on the ellipse according as x12/a2 + y12/b2 – 1 >, < or equal to 0.
Auxiliary circle of an Ellipse
Auxiliary circle of an ellipse which is a circle described on the major axis of an ellipse as its diameter.
Let the ellipse be
x2/a2 + y2/b2 =1 ...... (1)
Then the equation of its auxiliary circle is x2 + y2 = a2 ...... (2)
Take a point P(x1, y1) on (1).
Through P, draw a line perpendicular to major axis intersecting major axis in N and auxiliary circle in P'.
The points P and P’ are called as correspoding points on the ellipse and auxiliary circle respectively.
This angle is known as the eccentric angle of the poitn P on the ellipse and auxialiary circle respectively.
Parametric Representation
The coordinates x = a cos θ and y = b sin θ satisfy the equation x2/a2 + y2/b2 = 1, for all real values of θ.
Thus x = a cos θ, y = b sin θ are the parametric equations of the ellipse x2/a2 + y2/b2 = 1, where 0 ≤ θ ≤ 2π.
Therefore the coordinates of any point on the ellipse x2/a2 + y2/b2 = 1 may be taken as (a cos θ, b sin θ). The angle θ is called the eccentric angle of the point (a cos θ, b sin θ) on the ellipse.
Tangents to the Ellipse
The condition for the line y = mx + c to be a tangent to the ellipse x2/a2 + y2/b2 = 1 is that c2 = a2m2 + b2 and the coordinates of the points of contact are ± (a2m/√(a2m2 + b2), (- b2/√(a2m2 + b2).
Also, x cos a + y sin a = p is a tangent if p2 = a2 cos2α + b2 sin2α
Moreover, lx + my + n = 0 is a tangent if n2 = a2l2 + b2m2.
Fro more detalis on equations of tangent in different forms, stduents may refer the following sections.
Chord of Contact
The equation of chord of contact of atngent drawn from a point P(x1, y1) to the ellipse x2/a2 + y2/b2 = 1 is T = 0, where T = xx1/a2 + yy1/b2 -1.
.jpg "Chord of contact of ellipse")
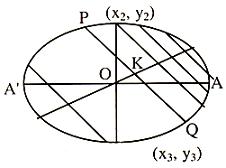
Diameter of an Ellipse
The locus of the middle points of a system of parallel chords of an ellipse is called the diameter of the ellipse.
Let y = mx + c ...... (1)
be the equation of a system of parallel chords of the ellipse x2/a2 + y2/b2 = 1 ...... (2)
In (1) m is constant and c varies from chord to chord. Let K (x1, y1) be the midpoint of a chord PQ of this system.
Eliminating y between (1) and (2) we get
(a2m2 + b2)x2 + 2a2mcx + a2(c2 - b2) = 0 ...... (3)
⇒ x2 + x3 = (-2a2 mc)/(a2 m2+b2 )
But x1 = (x2+x3)/2 =(-a2 mc)/(a2 m2+b2)
Or c = (-x(a2 m2+b2))/(a2 m2)
Also K (x1, y1) is a point on (1) so
y1 = mx1 + c ⇒ y1= -b2x1/a2m
.·. The locus of K (x1, y1) is y = -b2x/a2m which is a diameter of the ellipse x2/a2 + y2/b2 = 1.
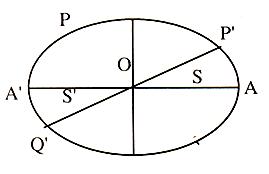
Conjugate Diameters
Two diameters of an ellipse which bisects chords parallel to each other are called conjugated diameters. Therefore the diameters y = mx and y = m1x of the ellipse x2/a2 +y2/b2 = 1 are conjugate if mm1 = -b2/a2.
Key Points:
-
In an ellipse, the major axes bisects all chords parallel to the minor axes and vice-versa, therefore major axes and minor axes of an ellipse are conjugate diameters but they do not satisfy the condition mm1 = -b2/a2 and are the only perpendicular conjugate diameters.
-
The eccentric angles of the ends of a pair of conjugate diameters differ by a right angle.
-
Equi-conjugate diameter: If the length of two conjugate diameters of ellipse be equal then they are called equi conjugate
diameters. -
The equation of equi conjugate diameters are x2/a2 ± y2/b2 = 1.
-
The eccentric angles of the ends of a pair of conjugate diameters of an ellipse differ by a right angle i.e., if one end of a diameter (PQ) is P(a sin Φ, b cos Φ).
-
The sum of the squares of any two conjugate semi-diameters of an ellipse is constant and equal to the sum of the squares of the semi-axis of the ellipse i.e. OP2 + OP2 = a2 + b2.
-
The produce of the focal distances of a point on an ellipse is equal to the square of the semi-diameters, which is conjugate to the diameter through the point.
-
The tangents at the ends of a pair of conjugate diameters of an ellipse form a parallelogram and the area of the parallelogram is constant and is equal to the product of the axis i.e. equal to 4ab.
Director circle of an Ellipse
The director circle is the locus of the point of intersection of pair of perpendicular tangents to an ellipse.
Two perpendicular tangents of ellipse x2/a2 + y2/b2 = 1 are
y - mx = √(a2m2+b2) ...... (1)
and my + x = √(a2+b2 m2) ...... (2)
To obtain the locus of the point of intersection (1) and (2) we have to eliminate m squaring and adding (1) and (2), we get
(y - mx)2 + (my + x)2 = (a2m2 + b2) + (a2 + b2m)
⇒ x2 + y2 = a2 + b2, which is the equation of the director circle.
How to find equation of a chord of an Ellipse whose mid point is (x1, y1)?
Let the ellipse be x2/a2 + y2/b2 = 1 ...... (1)
Any line through (x1, y1) is y - y1 = m(x - x1) ...... (2)
Eliminating y between (1) and (2) we get
x2 (b2 + a2m2) + 2ma2 (y1 - mx1) x + a2 [(y1 - mx1)2 - b2] = 0
If x2 and x3 are the roots of this equation then
x2 + x3 = -2ma2 (y1 - mx1)/(b2 + a2m2)
But (x1, y1) the mid point of the chord.
.·. x1 = (x2 + x3)/2 = (-ma2 (y1 - mx1 ))/(b2 + a2m2)
⇒ m = (-b2x1)/(a2y1)
.·. From (2) and (3) the equation of the chord where mid point is (x1, y1) is
y - y1 = ((-b2x1)/(a2y1)) (x - x1)
⇒ xx1/a2 + yy1/b2 = (x12)/a2 +(y12)/b2
Or T = S1 where T = xx1/a2 + yy1/b2 -1
and S1 = (x12)/a2 + (y12)/b2 -1
Pole and polar of an Ellipse
The locus of the points of intersection of tangents drawn at the point extremities of the chords passing through a fixed point is called the polar of that fixed point and the fixed point is called the pole.
Equation of the polar of P(x1, y1) with respect to the ellipse
x2/a2 + y2/b2 = 1 is
xx1/a2 + yy1/b2 = 1
Key Points:
-
Polar of the focus is the directirx.
-
Any tangent is the polar of its points of contact.
-
If the polar of P(x1, y1) passes through Q(x2, y2) then the polar of Q will pass through P and such points are siad to be conjugate points.
-
The point of intersection of any two lines is the pole of the line joining the pole of the two lines.
-
If the pole of the line lx + my + n = 0 lies on another line l’x + m’y + n’ = 0, then the pole of the second line will lie on the first and such lines are said to be conjugate lines.
Illustration:
How to find out pole of the line lx + my + n = 0 w.r.t. the ellipse x2/a2+y2/b2 = 1.
Solution:
Let (x1, y1) be the pole of line lx + my + n = 0. ...... (1)
w.r.t. the ellipse x2/a2 + y2/b2 = 1 ...... (2)
Now the polar of (x1, y1) w.r.t. (2) is xx1/a2 + yy1/b2 = 1 ...... (3)
Since (1) and (3) represents the same polar, so comparing them we have
(x1/a2)/l + (y1/b2)/b2 = (-1)/n
or x1 = (-a2 l)/n y1 = (-b2m)/n
.·. The required pole is ((-a2 l)/n,(-b2 m)/n)
Illustration:
The number of values of c such that the straight line y = 4x + c touches the curve x2/4 + y2 = 1 is ? (IIT JEE 1998)
Solution:
For an ellipse, we know that the condition for tangency is c2 = a2m2 + b2
The given line is y = 4x + c and the curve x2/4 + y2 = 1
hence, c2 = 4.42 + 1 = 65
Hence, c = √65.
Related Resources
-
Click here to refer the most Useful Books of Mathematics.
-
For getting an idea of the type of questions asked, refer the previous year papers.
-
Fast Track your revision with the ultimate Revision Notes on Ellipse.
To read more, Buy study materials of Ellipse comprising study notes, revision notes, video lectures, previous year solved questions etc. Also browse for more study materials on Mathematics here.